 Mandelbrot Mandelbrot
 The Mandelbrot set, is surely the most popular and well known fractal – probably the best known object in contemporary mathematics. Benoit Mandelbrot discovered it in 1979, and since then his experiment has been duplicated by tens of thousands of mathematicians around the world. Initially the computer generation of the Mandelbrot set took hours and produced a very inferior picture. These days, with the speed of modern computers, the wonderful complexities of the Mandelbrot set are revealed even as we watch. The Mandelbrot set, is surely the most popular and well known fractal – probably the best known object in contemporary mathematics. Benoit Mandelbrot discovered it in 1979, and since then his experiment has been duplicated by tens of thousands of mathematicians around the world. Initially the computer generation of the Mandelbrot set took hours and produced a very inferior picture. These days, with the speed of modern computers, the wonderful complexities of the Mandelbrot set are revealed even as we watch.
Mandelbrot is known as the creator of fractal geometry. He is one of the few living mathematicians whose originality has given birth to an entire discipline. He was largely self-taught, allowing him to think in unconventional ways and to develop a highly geometrical approach to mathematics. In 1958, Mandelbrot joined IBM, delving into processes with unusual statistical properties and geometric features. This led to his famous contributions in fractal geometry. His gives lectures which are lively, clear to the non-mathematical, and which can reach a memorable level for many who never imagined they would resonate with novel mathematics. Many of his discoveries have a surprising aesthetic value combined with an unexpected usefulness in teaching.
Applet
The best way to appreciate the beauty and complexities of the Mandelbrot set is to play with it. Here is a link to an applet of the Mandelbrot set. The author is Eckhard Roessel, and he has very kindly made his applet freely available. Check out his home page:
http://home.t-online.de/home/eckhard.roessel/
Place the applet window in the top right hand corner of your screen, so that you can see at least the bottom half of this page. If you use your mouse to drag out a rectangle in the window, the applet will zoom in on that part of the Mandelbrot set. A simple click on the window will restore the set to its original size.
Here are some simple exploratory exercises.
• Zoom in on the long straight ‘tail’ at the left of the Mandelbrot set. Show that miniature Mandelbrot sets keep occurring.
This demonstrates a basic fractal property: the whole original set appears again and again in miniature within the original figure.
• Look at the basic shapes in the Mandelbrot set. What name do we give the shape of the main solid region? What shape are the ‘buds’?
• On top of the cardioid (main region) is a big bud. Moving around clockwise, there is a next smaller ‘big bud’. Moving around clockwise, there is a further next smaller ‘big bud’. And so on. Zoom in on each of these in turn, allowing space for some of the filaments sprouting out. In each case, zoom in on the first visible black miniature Mandelbrot set on the main filament, allowing space for the lateral filaments to show. Count the number of main sprouts on these filaments. Do you find a pattern?
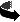

The Mandelbrot set is full of such patterns.
# You should have found in turn, 2, 3, 4, 5, ... main sprouts on each of the lateral filaments.
Take time to just play with the applet, exploring the many glorious patterns around the Mandelbrot set. There is a lot of mathematics here, but anyone can enjoy the beauty and intracacy of the designs.
Generation of the Mandelbrot set
To understand the Mandelbrot set, we need to understand complex numbers. These are numbers of the form z = x + iy where x, y are real, and i2 = –1. Number z can be represented in the complex plane by the point (x, y).
Now if c is a fixed complex number in the z-plane, let us consider the transformation of the plane under the mapping z  z2 + c. Each point z in the plane maps to a new point z2 + c. Suppose now we obtain a whole sequence of points by starting with a given z and carrying out this transformation repeatedly. Thus: z2 + c. Each point z in the plane maps to a new point z2 + c. Suppose now we obtain a whole sequence of points by starting with a given z and carrying out this transformation repeatedly. Thus:
It turns out that this sequence of points does one of two things. Either
(a) it remains in some bounded part of the plane (say within a circle of suitably large radius), or
(b) it ‘escapes to infinity’, getting further and further away from the origin.
You may well ask why mathematicians would be interested in this behaviour, but Benoit Mandelbrot’s inspiration was to extend this idea to what is called ‘the c-plane’. That is, instead of choosing a fixed value of c, let us consider let us choose a whole plane full of cs, where each c of course is a complex number. Now for each choice of c, apply the transformation (*). That is, consider
If this sequence of points escapes to infinity, we colour the point c black. Otherwise we colour the point c white. The set of black points is the Mandelbrot set.
 We can make several observations about this. Mandelbrot’s original computed sketch was very scrappy. Generation of the Mandelbrot set takes up an enormous amount of computing power and time – at least with an old machine. The calculation (**) has to be performed for every point in the c-plane, or at least in part of it. Furthermore, the sequence may escape to infinity very slowly, so how many iterations are required? We can make several observations about this. Mandelbrot’s original computed sketch was very scrappy. Generation of the Mandelbrot set takes up an enormous amount of computing power and time – at least with an old machine. The calculation (**) has to be performed for every point in the c-plane, or at least in part of it. Furthermore, the sequence may escape to infinity very slowly, so how many iterations are required?
With modern versions, the background of the drawing often appears coloured. The colours are usually chosen to correlate with the speed at which points not belonging to the Mandelbrot set escape to infinity.
A final surprise
In 1991 Dave Boll was carrying out a small computer experiment, trying to verify that the ‘neck’ of the Mandelbrot set (that is, the join between the heart and the biggest bud) has, in fact, zero thickness. The neck of the Mandelbrot set actually lies at the point (–0.75, 0). So he was testing points –0.75 + yi, where y is a small number, seeing how many iterations were required before the point ‘escaped’ (beyond some fixed circle). He obtained these values:
|
y
|
Iterations
|
|
0.1
|
33
|
|
0.01
|
315
|
|
0.001
|
3143
|
|
0.0001
|
31417
|
|
0.00001
|
314160
|
|
0.000001
|
3141593
|
|
0.0000001
|
31415928
|
Boll thought the number of iterations was starting to look remarkably suspicious. Can you see why? His reaction was: What the HELL is  doing here?! doing here?!
It is clear that there is some quite deep mathematics here, and we have hardly touched on the mysteries of the Mandelbrot set. Hopefully you have been encouraged to dig deeper.
Bibliography
Fractals for the Classroom, Peitgen, H-O., Jürgens, H., Saupe, D. (Spinger-Verlag 1992)
|
 Mandelbrot
Mandelbrot The Mandelbrot set, is surely the most popular and well known fractal – probably the best known object in contemporary mathematics. Benoit Mandelbrot discovered it in 1979, and since then his experiment has been duplicated by tens of thousands of mathematicians around the world. Initially the computer generation of the Mandelbrot set took hours and produced a very inferior picture. These days, with the speed of modern computers, the wonderful complexities of the Mandelbrot set are revealed even as we watch.
The Mandelbrot set, is surely the most popular and well known fractal – probably the best known object in contemporary mathematics. Benoit Mandelbrot discovered it in 1979, and since then his experiment has been duplicated by tens of thousands of mathematicians around the world. Initially the computer generation of the Mandelbrot set took hours and produced a very inferior picture. These days, with the speed of modern computers, the wonderful complexities of the Mandelbrot set are revealed even as we watch.
 We can make several observations about this. Mandelbrot’s original computed sketch was very scrappy. Generation of the Mandelbrot set takes up an enormous amount of computing power and time – at least with an old machine. The calculation (**) has to be performed for every point in the c-plane, or at least in part of it. Furthermore, the sequence may escape to infinity very slowly, so how many iterations are required?
We can make several observations about this. Mandelbrot’s original computed sketch was very scrappy. Generation of the Mandelbrot set takes up an enormous amount of computing power and time – at least with an old machine. The calculation (**) has to be performed for every point in the c-plane, or at least in part of it. Furthermore, the sequence may escape to infinity very slowly, so how many iterations are required?