|
London London is one of the four largest cities in the world, has a population of over 8 million, and is famous for many things: Buckingham Palace, the Houses of Parliament and Big Ben, ‘London Bridge’, and the Tower amongst others. It is a fascinating mix of old and new. Visitors love its historic buildings, its many churches, its beautiful parks, the Thames River crossed by many bridges, the pigeons in Trafalgar Square. For many, a visit to London is a return to one’s roots, a fleeting glimpse of the past, a renewed association with names and places vaguely remembered from school days, but never before appreciated. One can spend literally months walking the streets, each day finding some new treasure, making some new discovery. Of course there is also the traffic, the crowds, the litter, the pollution, ... . But somehow these are soon overlooked and forgotten – accepted as an inevitable part of this thriving, sprawling metropolis. |
|
The Underground map (I)
Even at this small scale, we see that the Underground map, based on an idea of Harry Beck, is not an accurate representation. The railway lines are certainly not straight as indicated, nor are the stations equally spaced. Your city may have a similar transport map. For a detailed map of the London Underground see |
|
Dimension You will observe from the Underground map that three lines intersect at Oxford circus. This might bring to mind a vision of some form of Russian Roulette, with trains whizzing by, perhaps missing by a hair’s breadth. Of course this does not happen.
The Underground lines are at various levels below ground. Because the map is a ‘flat’ picture, this fact is not apparent. This illustrates the importance of the mathematical concept of dimension. We know that we live in a ‘3-dimensional’ world. But what does this mean? 6. (a) What do you understand by the word ‘dimension’? How would you explain this to a pre-school child? Why do we live in a three dimensional world?
|



 The Underground
The Underground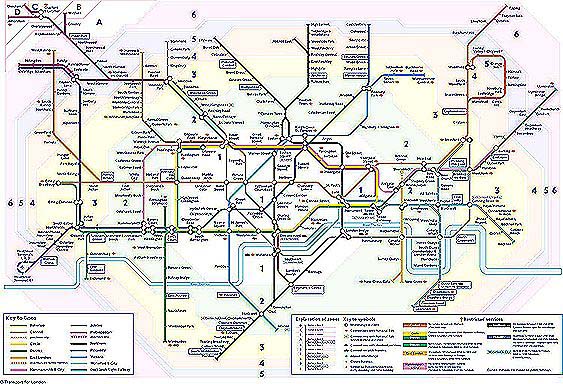
 Topology
Topology 4. (a) The map shows the stations Tufnell Park, Kentish Town and Camden Park lying consecutively on the Northern Line. If travelling from Tufnell Park to Camden Park, would you expect the train to pass through Kentish Town? Why? What property is preserved here?
4. (a) The map shows the stations Tufnell Park, Kentish Town and Camden Park lying consecutively on the Northern Line. If travelling from Tufnell Park to Camden Park, would you expect the train to pass through Kentish Town? Why? What property is preserved here?