|
The Great Pyramid and pi
At right is another relationship apparent in the Great Pyramid:
|
“the perimeter of the square base is equal to the circumference of a circle having radius equal to the height of the pyramid.”
|
  Investigate Investigate
Given that the base length of the Pyramid is 2, and the height, as in the previous slide is  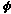 , show that , show that   4/ 4/ 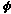 . Check the accuracy of this with your calculator. . Check the accuracy of this with your calculator.
 Investigate Now substitute the royal cubit measures of the base perimeter and the height of the Pyramid (given above) in this relationship, to show Investigate Now substitute the royal cubit measures of the base perimeter and the height of the Pyramid (given above) in this relationship, to show   22/7. 22/7.
 Investigate Yet another relationship discovered elsewhere in Ancient Egyptian monuments is the approximate result: Investigate Yet another relationship discovered elsewhere in Ancient Egyptian monuments is the approximate result:   6/5. 6/5.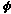 2. Check this using your calculator. 2. Check this using your calculator.
Good approximations to 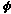 are given by the ratios of successive terms of the Fibonacci series 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... . We can get get a good approximation to are given by the ratios of successive terms of the Fibonacci series 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... . We can get get a good approximation to  in terms of these. With a circle of diameter 21 units, the circumference is in terms of these. With a circle of diameter 21 units, the circumference is
21  21.6/5 21.6/5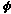 2 = 21.6/5. 2 = 21.6/5.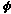 . .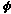  21.6/5.34/21.55/34 = 66. 21.6/5.34/21.55/34 = 66.
|
This gives an approximate value of  as 66/21 = 22/7. as 66/21 = 22/7.
|
|
|




 The pyramids (II)
The pyramids (II)



