|
HYPERCUBES
We now look at a different sequence of objects. Again the figures we get will be skeletal, in the sense that the construction will give the vertices and edges of each figure. In 0 dimensions we have a point. (That is still all there is.) In 1 dimension, we take the point and move it unit distance, drawing in the trace path of the vertex, to obtain a line segment. In 2 dimensions, we take the line segment and move it a unit distance perpendicular to itself, drawing in the trace paths of the vertices, to obtain a square. In 3 dimensions, we take the square and move it a unit distance perpendicular to itself, drawing in the trace paths of the vertices, to obtain a cube. The general figure defined in this way is called a hypercube. If you want to specify the dimension d, you can speak of a d - hypercube. For example a cube is a 3-hypercube.
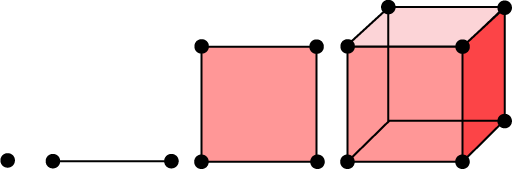
The first four members of the sequence of figures we obtain will look like this (we have added some shading for the faces):
How would we picture the 4-dimensional hypercube? Again there are several options: we could construct a 3-dimensional model, or draw a 2-dimensional picture. First of all, look at the picture of the cube above (right). We can ‘see’ that this represents a cube because we know what a 3-dimensional cube looks like. But really, it is just a 2-dimensional picture. We can think of it as two congruent and similarly placed squares with corresponding vertices joined together.
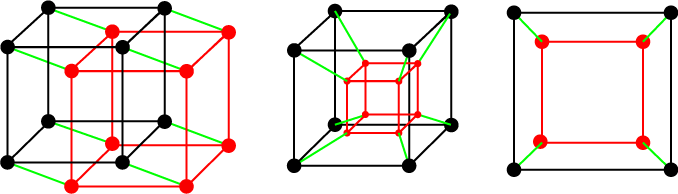
To obtain the 3-dimensional representation, we take a two cubes which are similarly placed, and join each pair of corresponding vertices. The figure at left below gives a picture with congruent cubes. A neater picture (and one which produces a nice model when made of struts and joiners) has one cube inside the other, as in the central figure below. You can think of this model having some perspective! After all, you can represent a cube quite realistically in the same way with one square inside the other (see figure at right below).
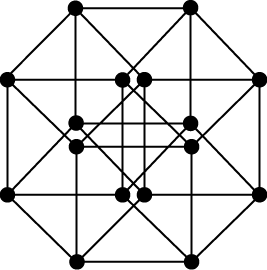
Of course, each of the above pictures of the 4-hypercube is automatically a 2-dimensional representation. One of the prettiest such figures is given below.
Let us now proceed for the hypercubes as we did with the simplexes, investigating whether there are nice relationships between the quantities V, E, F and C. We work with the extended table we introduced for the simplexes (deciding that the effort is worthwhile!).
Your completed table should look like this:
It is easy to fill in the top two rows, the diagonal of 1s, and the zeros. After filling in the top two rows, each non-zero entry is the sum of twice the entry to its left and the entry above that. This means that we can fairly confidently give the values for a hypercube of any dimension. Again this doesn’t prove that these results are the correct ones. But looking back on our method of construction, we can understand where the factor 2 comes from. Let us check our extended Euler’s Formula. For the line segment : V = 2. A nice sequence of 2-dimensional representations from the 2-hypercube (square) to the 7-hypercube is given in Wolfram Math World (reference and link below):
In 1 dimension, a line segment of (edge-) length 2 can be represented algebraically by In 2 dimensions, a square of edge-length 2 can be represented by In 3 dimensions, a cube of edge-length 2 can be represented by It is not hard to guess the representation for further members of the sequence!
Thus in 2 dimensions (the plane), we denote the square by {4}. In 3 dimensions, we denote the cube by In 4 dimensions, we denote the hypercube by In general d-dimension
The hypercube in 4 dimensions is sometimes called a tesseract (the Greek tesseres means ‘four’). You might recall that the model of the cube can be constructed from a net of six squares. The analogue for the 4-hypercube would be a ‘net’ of eight cubes, as shown below. You may have some trouble folding them! This does make a nice 3-dimensional model though.
Abbott, E. A., Flatland, a romance of many dimensions, Dover (Edition 6) 1953. (The full text of this delightful classic is now available online: http://www.ibiblio.org/eldritch/eaa/FL.htm .) Coxeter, H.S.M., Introduction to Geometry, Wiley 1969. (See Chapter 22.) Coxeter, H.S.M., Regular Polytopes, 2nd Edition (Macmillan 1963). (This is more of a specialist book.) Wikipedia: http://en.wikipedia.org/wiki/Tesseract Wolfram Math World : http://mathworld.wolfram.com/Hypercube.html |

 We won’t try to justify this in general, but in the case of the cube the faces are square {4}s, with 3 meeting at each vertex. Or, we can say that each vertex figure is an equilateral triangle {3}. In 4 dimensions, the cells are cubes
We won’t try to justify this in general, but in the case of the cube the faces are square {4}s, with 3 meeting at each vertex. Or, we can say that each vertex figure is an equilateral triangle {3}. In 4 dimensions, the cells are cubes 
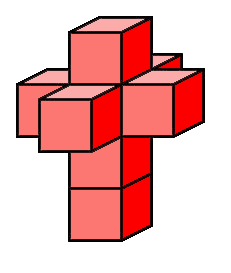
 It is interesting that this configuration of cubes is used by Salvador Dali in his 1954 painting Crucifixion or Corpus hypercubicus. A host of literary and film references to the 4-hypercube is given in
It is interesting that this configuration of cubes is used by Salvador Dali in his 1954 painting Crucifixion or Corpus hypercubicus. A host of literary and film references to the 4-hypercube is given in