3. ELEMENTARY
FUNCTIONS 
|
|
|
Exponential and Trigonometric Functions
|
 |
 |
If z = x + iy, we define the exponential function exp z = ex cis y (= ez).
Notes
1. We can give an alternative definition in terms of power series.
Writing out a formal series for e iy gives cis y.
2. If y = 0, then exp z = exp x = ex. Thus the complex exponential function naturally extends the real function.
3. In this definition, y is in radian measure.
|
|
Properties of the Exponential (II)
|
 |
 |
If y is a real number, we have
exp(iy) = cos y + i sin y,
exp(–iy) = cos y – i sin y,
cos y = 1/2. (exp(iy) + exp(–iy)),
sin y = 1/2i.(exp(iy) – exp(–iy)).
Thus it is natural to define cosine and sine as:
cos z = 1/2. (exp(iz) + exp(–iz)),
sin z = 1/2i.(exp(iz) – exp(–iz)).
These are Euler's relations. Again notice here how we try to generalize, or extend, a ‘real’ situation to the complex case.
|
|
Properties of Sine and Cosine
|
 |
 |
1. Both functions are entire:
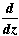 (sin z) = cos z, (sin z) = cos z, 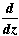 (cos z) = – sin z. (cos z) = – sin z.
2. Both functions are periodic, of period 2 . This follows from the periodicity of the exponential function. . This follows from the periodicity of the exponential function.
The functions satisfy the usual identities, as in the real case.
3. sin2 z + cos2 z = 1.
4. sin(z1 + z2) = sin z1 cos z2 + sin z2 cos z1 etc.
5. sin(– z) = – sin z, cos(– z) = cos z etc.
Does the exponential function have an inverse logarithmic function? Since the exponential function is periodic, any inverse would have to be multi-valued. Let us write
w = log z  z = exp w. z = exp w.
If we set z = r cis 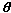 , w = u + iv, then r cis , w = u + iv, then r cis 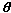 = eu cis v. = eu cis v.
From this, we deduce that
r = eu, u = ln r, v = 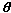 + 2k + 2k . .
Thus there are infinitely many values of log z, the different values differing by 2k i. Each value of k gives a branch of the logarithm. i. Each value of k gives a branch of the logarithm.
|
|
|
|
|
1. A path which crosses the cut moves to the next branch.
|
|
2. If z is real and positive, then Log z = ln r.
|
|
3. We can think of the branch planes interleaved together, with the x-axis as a common axis. A path drawn about the origin in one branch plane reaches the cut and then passes to the next branch plane.
|
|
4. Our choice of the positive x-axis for the cut was somewhat arbitrary. Other branch cuts are possible; but O is common to them all – O is a branch point.
|
|
|
Properties of the Logarithm (I)
|
 |
 |
These functions are continuous on the given domain and satisfy the Cauchy-Riemann equations there. Hence by Theorem 2.5, Log z is analytic.
[Note There is a problem in defining arctan here when x = 0. We could overcome this by defining 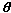 = arccot x/y, or by taking time to develop a polar form of the Cauchy-Riemann equations.] = arccot x/y, or by taking time to develop a polar form of the Cauchy-Riemann equations.]
|
|
Properties of the Logarithm (II)
|
 |
 |
All branches have the same derivative, since they differ by a constant.
3. Inverse Property
exp(log z) = z (for any branch)
log(exp z) = z (for a particular branch).
log z1 + log z2 = log(z1 . z2)
log z1 – log z2 = log(z1 / z2)
providing we choose the appropriate logarithm branch on the right.
|
|
Examples on the Logarithm
|
 |
 |
| Example 1. Evaluate Log(–1) + Log(–1).
Now –1 = 1 . cis  , so Log(–1) = 0 + i , so Log(–1) = 0 + i . .
Hence 2Log(–1) = 2 i = log 1, but not Log 1 (= 0). i = log 1, but not Log 1 (= 0).
|
Using our knowledge of real powers, we define the complex power zc (c 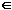 C) by C) by
zc = exp(c log z), (z  0). 0).
Since zc is defined in terms of the logarithm, we expect zc to be multivalued, so we use the cut plane as for the logarithm. Then since log z is single-valued and analytic in the cut plane, so is zc. Now
|