7. RESIDUES
AND POLES 
|
Definition If there exists a neighbourhood of z0 throughout which f is analytic except at z0 itself, then z0 is an isolated singularity of f.
Example  has three isolated singularities: z = 0, z = has three isolated singularities: z = 0, z = i. i.
Contrast Log z which has a continuous ray of singularities.
Now from the Cauchy integral formula and the Derivative formulae,
where the integrals are in an anti-clockwise direction about a simple closed contour containing z0. We observe that the values of these integrals are of the form 2 i.K. i.K.
We now change our notation, replacing f(z) / (z – z0) by f(z).
So denote by f(z) a function which is analytic on and inside C except at an isolated singular point z0 inside C.
Then 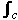 f(z) dz = 2 f(z) dz = 2 i.K, where K is a constant and the integral is once anti-clockwise round C. i.K, where K is a constant and the integral is once anti-clockwise round C.
Definition 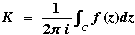 is the residue of f at the isolated singular point z0. is the residue of f at the isolated singular point z0.
Theorem 7.1 (Residue Theorem) Let C be a closed contour within and on which function f is analytic except for a finite number of singular points z1, z2, ... , zn interior to C. If Ki denotes the residue of f at zi, then
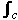 f(z) dz = 2 f(z) dz = 2 i.(K1 + K2 + ... + Kn), i.(K1 + K2 + ... + Kn),
where the integral is around C in positive sense.
|
|
Proof of the Residue Theorem
|
 |
 |
Proof Let each zi be enclosed as shown in a circle Ci with radius small enough so that C and Ci are all separated. Now f is analytic in the remaining region within and including C, so by Cauchy's Theorem:
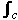 f(z) dz – f(z) dz – 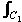 f(z)dz – ... – f(z)dz – ... – 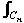 f(z)dz = 0, f(z)dz = 0,
so 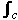 f(z) dz = f(z) dz = 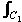 f(z)dz – ... – f(z)dz – ... – 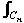 f(z)dz f(z)dz
= 2 i.(K1 + K2 + ... + Kn), i.(K1 + K2 + ... + Kn),
using the definition of Ki.
It follows that evaluation of such integrals depends on our ability to evaluate residues.
|
|
Example on the Residue Theorem
|
 |
 |
Evaluate  , where C is | z | = 2 taken in the positive sense. , where C is | z | = 2 taken in the positive sense.
The singularities inside C are z = 0, 1. So I = 2 i.(K0 + K1) (say). i.(K0 + K1) (say).
Find K0. Set g(z) = (5z – 2)/(z – 1) – analytic in a small circle C0 centred at 0.
By the Cauchy integral formula, 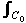 g(z)/z dz = 2 g(z)/z dz = 2 i.g(0) = 2 i.g(0) = 2 i.2 = 2 i.2 = 2 i.K0. i.K0.
(1) Use partial fractions:
(2) Use the Laurent expansion with | z | > 1, and find the coefficient of 1/z. So
and noting that the coefficient of 1/z is 5, we obtain the result as before.
Singularities are obviously important in the theory. The nature of a singularity can be determined from the Laurent expansion
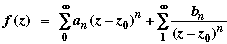 (over some domain) (over some domain)
(3) Consider f(z) = sin z / z .
Here 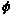 (z) = sin z is analytic, but (z) = sin z is analytic, but 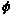 (0) = 0. Hence this is not a simple pole. In fact (0) = 0. Hence this is not a simple pole. In fact
We say z = 0 is a removable singularity. We could define f(0) = 1. (This would give a new function, coinciding with f for z 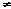 0, but also defined at z = 0 and continuous there.) 0, but also defined at z = 0 and continuous there.)
(4) Consider f(z) = e1/z. There is a problem here at z = 0. Assuming
it is not possible to put this in the form 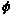 (z)/zm for any m. We call this an essential singularity. (z)/zm for any m. We call this an essential singularity.
(1) We can give general formulae for the residues for poles of order m – essentially using Theorems 6.3, 6.4.
(2) Work on series is useful here.
(3) Most examples treat poles of low order. It is suggested that you learn the Cauchy integral formula and the Rules on Differentiation with respect to z0. Thus:
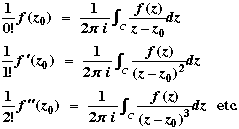
|
|
More Examples on Poles and Residues
|
 |
 |
(1) Consider  . .
This function has a pole of order 3 at z = 0.
Hence the residue there is 1/2! . f ''(0) = 1/2! . 4 . e0 = 2.
(2) Consider 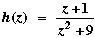 . .
This function has a simple pole at z = 3i.
The residue there is
|
|
Improper Real Integrals: Cauchy Principal Value
|
 |
 |
In the case of real improper integrals, we make the definition:
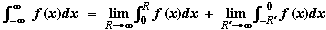 (1) (1)
where both integrals on the right exist. Notice that the variables R, R' tend to infinity independently in the two integrals.
It is useful to define the Cauchy Principal Value (Cauchy P.V.) in the following way:
 (2) (2)
So with the Cauchy P.V., we are insisting that the upper and lower infinite limits are approached at the same rate.
If the improper integral defined by (1) converges, then the value obtained is the Cauchy P.V. On the other hand, the Cauchy P.V. may exist and integral (1) not converge.
|
|
Using the Cauchy Principal Value
|
 |
 |
Example Let f(x) = x. Here the Cauchy P.V. is 0, but the integral is not convergent.
Special case If f is even and the Cauchy P.V. exists, then  converges. converges.
For in this case
and the existence of the last Cauchy P.V. guarantees the existence of the first two integrals.
Example If f(x) = p(x) / q(x) where p, q are real polynomials with no common factors, q(x) has no real zeros, and the degree of q(x) is greater than or equal to the degree of p(x) + 2, then  converges. Its value can easily be found using residues. converges. Its value can easily be found using residues.
|
|
Cauchy Principal Value: Example (I)
|
 |
 |
|
|
Cauchy Principal Value: Example (II)
|
 |
 |
and the length of CR is  R. Thus R. Thus
So  = =  /100 (noting that f is even), or I = /100 (noting that f is even), or I =  /200 . /200 .
Question Is this easier than factorizing and using partial fractions in the real case?!
Probably yes, especially as the integral around CR will fairly clearly always vanish when the difference in degree is 2 or more.
|
|
Improper Integrals involving Trigonometric Functions
|
 |
 |
Residue theory is also useful for evaluating integrals of the form
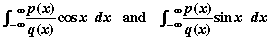 (*) (*)
where p, q are real polynomials and q(x) has no real zeros.
Note that the previous method cannot be used here. For we have
| sin z |2 = sin2 x + sinh2 y and | cos z |2 = cos2 x + sinh2 y,
so | cos z | and | sin z | increase like sinh y as y  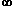 . .
However, the integrals (*) can be combined to give
 , ,
and | e iz | = e – y, which is bounded in the upper half plane.
|
|
Trigonometric Function Integral: Example (I)
|
 |
 |
Now 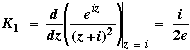 (calculating). (calculating).
[Continued]
|
|
Trigonometric Function Integral: Example (II)
|
 |
 |
We show that the second integral tends to 0 as R  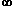 . For z in CR, . For z in CR,
Since the integrand is even here, this Cauchy P.V. is the required integral.
|
|
Definite Integrals of Trigonometric Functions
|
 |
 |
We can use residues to evaluate certain definite integrals of the type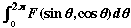 . .
That is, a contour integral of a function of z around the circle C in the positive sense.
|
|
Integrals of Trigonometric Functions: Example (I)
|
 |
 |
Show that 
The formula is valid for a = 0. Suppose that a 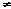 0. Then 0. Then
where C is the circle | z | = 1 traversed in the positive direction.
The denominator has zeros:
Hence the integrand is 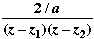 . .
|
|
Integrals of Trigonometric Functions: Example (II)
|
 |
 |
Also, noting that | a | > 1, we have | z2 | = (1 + 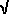 (1 – a2)) / |a| > 1; (1 – a2)) / |a| > 1;
that is, z2 lies outside C.
Further, | z1z2 | = 1, so | z1 | < 1, – a simple pole inside C.
The corresponding residue K1 is:
Hence I = 2 i.K1 = 2 i.K1 = 2 / /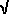 (1 – a2) . (1 – a2) .
Because of time constraints, the course finished here. With a little more time, we would have showed that analytic mappings are conformal (preserve angle measure), and worked through a few boundary value problems. These would have demonstrated again the practical nature of complex analysis, and given us practice in the use of complex mappings.
|