|
ASTROID : Generation
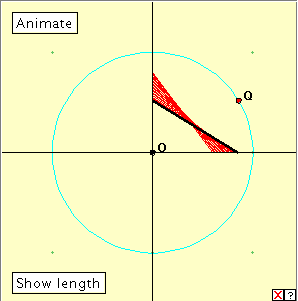
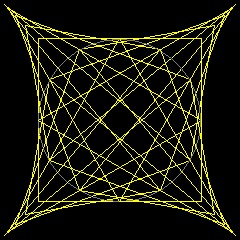
The applet linked to the diagram below generates the astroid. This is the simplest construction based on a pair of rectangular axes. Click on the diagram to open the applet, and then click on the ‘Animate’ button to generate the astroid. Click the button again to stop the generation. Clicking the little red x at bottom right will clear the drawing from the applet window. Now drag the red point Q slowly around the circle. Can you describe the construction? Click on the ‘Show Length’ button to check your answer. We have measured the segment length in pixels here. The small variation is caused by the programming calculations. Reflection Suppose we consider a segment of fixed length with endpoints on the x- and y- axes. As we slide this segment through all its possible positions, it determines the astroid as its envelope. A variation of the astroid is obtained by taking the two axes to be oblique. Occurrences
|
This simple but attractive curve seems to have acquired its present name of astroid only in 1838, in a book published in Vienna. Up until that time it had been called a cubocycloid, a paracycle, a four-cusp-curve, and various other names. The curve itself had been studied from much earlier times. For example we know that Leibniz had studied the curve by 1715.
