|
CARDIOID : Exploration
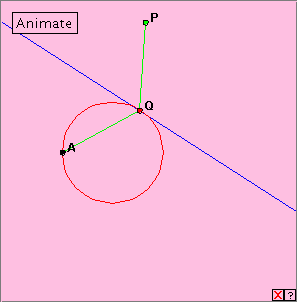
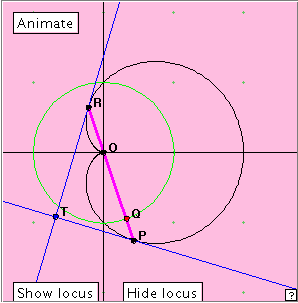
r = 1 + cos In this equation, r gives the distance from the origin (cusp) A to a general point P of the cardioid, and (x2 + y2 – x)2 = x2 + y2. We observe that the above cardioid intercepts the positive x-axis at x = 2, and the y-axis at y = Initially we generated the cardioid as an envelope of circles. The construction involved a given base circle of diameter 1/2. However, we did observe that the cardioid also occurs as the locus of points which are reflections of A in the tangent lines to the base circle. Here is an applet which demonstrates this property. Click on the adjacent figure, and run the applet using the ‘Animate’ button and manually by dragging point Q around the circle. What is the relationship between segments AQ and PQ? How do they relate to the blue tangent line? State a result about the generation of the cardioid. Take any circle through point A. Then the cardioid is the locus of the reflections of point A in the tangents to that circle. The cusp is obviously a very special point of the cardioid. Suppose that PR is a chord which passes through the cusp. Does this chord have any special properties? Run the adjacent applet using the ‘Animate’ button and manually. Think about the length of this chord. Remembering where the cardioid cuts the axes, what is the length of this chord in the horizontal position? the vertical position? Can you make a conjecture? Can you prove it? The cusp chord always has length 2. We can calculate this using the r-values of P and R: Length = (1 + cos What appears to be true about the tangents? What can you conjecture about the angle at T?
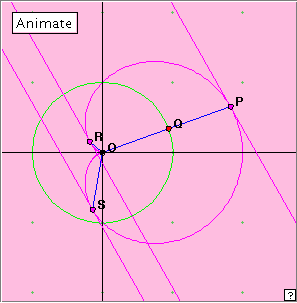
We saw above how the tangents at the end points of a cusp chord meet at right angles on a circle. In fact, the normals to the tangents at the end points have the same property, although the circle is different. Look carefully at the applet illustrated at right. You will probably find it most helpful to manually move the point Q. Concentrate on the endpoints P, R of the cusp chord. The tangents give two edges of the yellow rectangle meeting on the large circle as before. Now look at the other two adjacent sides, PN, RN. How are these related to the cardioid? The point N appears to move on a circle. Describe this circle. What is its centre? radius? We observe that edges PN, RN are perpendicular. In fact we know already that this must be the case (why is this?). The locus of point N is a circle which has center (0.5, 0) (the same centre as the large circle) and radius 0.5. The tangents and normals define a rectangle of changing shape which has two opposite vertices on the cardioid, and the remaining two opposite vertices lying on two concentric circles. Very pretty! In the diagram at right, we have three points P, R, S on the cardioid. Play with the applet to see what you can discover about this situation. What appears to be true about the three tangents? Would you expect there to be four tangents with this property? If P, R, S are three points on the cardioid with OP, OR, OS making equal angles of 2 |
 Properties
Properties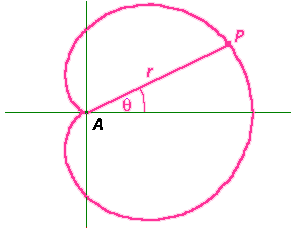 placed at the origin. The easiest way to represent the cardioid is by its polar equation:
placed at the origin. The easiest way to represent the cardioid is by its polar equation: