|
CARDIOID : Generation
We might observe that the shape of the cardioid is rather different from the traditional shape of the heart symbol The applet linked below generates the cardioid. The generation uses a fixed base circle, and a fixed point on it. Click the linked diagram below and then the ‘Animate’ button to generate the cardioid. Click the button again to stop the generation. Clicking the little x at bottom right will clear the drawing from the applet window. Now drag the red point slowly around the circle. Can you describe the construction? Reflection
Let us suppose that points Q, Q' are the centres of two circles through A which meet again at point P. The two triangles PQQ', AQQ' are clearly congruent (S. S. S.) Hence we can think of point P as the image of A under reflection in the line QQ'. Moving Q' around the circle until it coincides with Q means that in the limit, line QQ' becomes tangent to the circle, and P becomes a point on the cardioid. Thus another way of constructing the cardioid is to take the locus of points which are reflections of A in the tangent lines to the base circle. Occurrences
|
 The name ‘cardioid’ means heart-shaped (from the Greek: kardia = heart and eidos = shape). The term was first used by Castillon in The Philosophical Transactions of the Royal Society in 1741. However, others had studied the curve before him. The curve has one sharp point, the indented cusp. [A cusp is a point on the curve which has an infinite number of tangent lines. Can you see this here?]
The name ‘cardioid’ means heart-shaped (from the Greek: kardia = heart and eidos = shape). The term was first used by Castillon in The Philosophical Transactions of the Royal Society in 1741. However, others had studied the curve before him. The curve has one sharp point, the indented cusp. [A cusp is a point on the curve which has an infinite number of tangent lines. Can you see this here?]
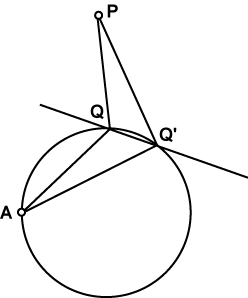 This method of generating the cardioid creates an envelope of circles, thus determining the shape.
This method of generating the cardioid creates an envelope of circles, thus determining the shape. 
