|
CATENARY : Exploration
f(x) = cosh x = ( A more general form which allows for some scaling is f(x) = c cosh (x/c). Although there are a couple of relationships with other standard curves (we shall look at these later), surprisingly the catenary appears to have no intrinsic properties of interest.
Bibliography A Book of Curves, Lockwood, E. H., (CUP 1967). Wikipedia : http://en.wikipedia.org/wiki/Catenary Wolfram MathWorld : http://mathworld.wolfram.com/Catenary.html |
As we have seen, the Cartesian equation of the catenary is given by the hyperbolic cosine function which is the average of two exponential functions: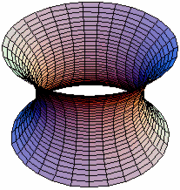
In 1744, Euler proved that the catenary is the curve which, when rotated, gives the surface of minimum surface area (the catenoid) for the given bounding circle.