In this section we give java applets which generate some of the caustic curves of each of our curves.
Caustic curves occur naturally in connection with reflected (refracted) light. Let F be a fixed point, called the radiant point, and let S be a given curve. Now if rays from F are reflected in S, then the envelope of the reflected rays is called the caustic of S having F as radiant point.
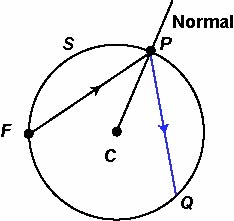We can express this more geometrically as follows. Let P be a variable point of the curve S, and let QP be drawn so that lines FP, QP make equal angles with the normal to the curve at P. Then the envelope of QP is the caustic.
The curve we have just defined is sometimes called the catacaustic, to distinguish it from another curve (the diacaustic) formed by the refracted rays. We will use the word caustic to mean catacaustic.
One of the best places to view a caustic curve is in the reflection of light on the surface of liquid cointained in a circular cup or bowl.
It is easy to construct the applet for the caustic. For each of curves we have constructed the normal to a tangen in generating the evolute. So beginning with these applets, we construct the normal at the point of intersection with the curve, form line OP (or more generally KP ), and then construct the reflection of OP in the normal.
Bibliography
A book of curves, Lockwood, E. H. (Cambridge University Press 1967).
