|
 The circle is a simple curve which has some particular interest in the generation of caustic curves.
Click the linked diagram below, and then click the ‘Animate’ button to generate the caustic curve of the circle with respect to the point Q. Clicking the little red x which appears at bottom right will clear the drawing from the applet window. Can you describe the construction? Experiment with different positions of the point Q. There are two cases of special interest, the first is when Q lies on the circle. What is the caustic curve in this case? For the second, drag the point Q as far right as you can on your computer monitor (that is, drag it outside the little applet window in the direction of the positive x-axis). What is the caustic curve in this case?
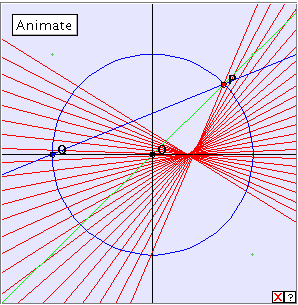
When Q lies at the centre of the circle, the construction degenerates. Can you explain why this happens? When Q lies on the circle, the caustic curve is a cardioid. When Q is ‘at infinity’ the caustic curve is a nephroid. This suggests a family connection between these two curves – a connection which is not surprising, considing their similarities of shape.
A Book of Curves, Lockwood, E.H. (Cambridge University Press, 1967) page 185.
|