CYCLOID : Caustic Curve
We recall the cycloid as the path traced out by a point on a circle rolling along a straight line. To find the caustic curve of the cycloid relative to the point K, we draw the line from K to point P on the curve, and then reflect this line in the normal to the curve at this point. The reflected lines generate the caustic as an envelope.
Click the linked figure below, and then click the ‘Animate’ button to generate the pedal curve of the cycloid. Click the button again to stop the generation. You can also see the construction by manually dragging the green point Q along the x-axis. Do you understand the construction? Do you recognize the caustic curve? Try it out for different positions of the point K on the y-axis. What happens when you drag K down to the bottom of your monitor (outside the applet window)? You will have to refresh your web page to locate point K again!
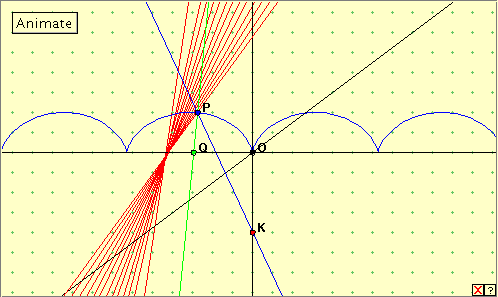
For a general position of point K we appear to obtain rather irregular cycloid-like curves. When K is ‘at infinity’ on either end of the y-axis (making the lines through it parallel to the y-axis), the caustic in fact becomes a cycloid of just half the dimensions of the given cycloid. It has two cycloidal arches tucked into each arch of the original cycloid.
Notice that this is another situation where the normal at the point P on the curve passes through the generating point Q. Why is this so?!
Bibliography
A Book of Curves, Lockwood, E. H. (Cambridge University Press, 1967), page 185.
|