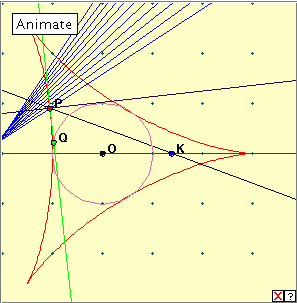
We have already looked at the deltoid as a type of three-pointed ornamental star. As usual, to find the caustic curve relative to radiant point K, we take a general point P on the curve, and then reflect the line KP in the normal at P. These reflected lines generate the caustic as an envelope.

Click on the diagram below to open the applet, and then click on the ‘Animate’ button to generate the caustic curve of the deltoid. Clicking the little red x at bottom right will clear the drawing from the applet window. Now drag the green point Q once slowly around the circle. Can you describe the caustic curve construction? Is this a curve we have seen before? Experiment with different positions of point K on the x-axis. In particular you might look at the cases where K is at the centre, at a cusp, or ‘at infinity’ (drag the point K as far right as you can on your monitor, and outside the applet window).