|
In this case we take the ellipse as a point locus, and construct the normal at each point P of the curve. If K is some fixed point, join KP, and reflect this line in the normal at P. The envelope of these reflected lines is the caustic with K as radiant point.
Click the linked diagram below, and then click the ‘Animate’ button to generate the caustic curve of the ellipse relative to point K. Clicking the little red x which appears at bottom right will clear the drawing from the applet window. Now drag the red point Q slowly around the circle. Notice that we have some choice in the position of the point K. You may be especially interested in looking at the cases when K lies on the ellipse (two positions) and when K lies at a focus (O ). Also investigate what happens when K lies ‘at infinity’ on the x-axis. (Drag the point K outside the applet window to the edge of your monitor. Refresh the page to retrieve K!)
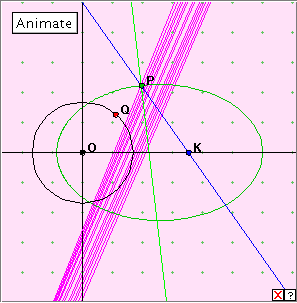
The caustic curves here are pretty but unfamiliar. They tend to have a cusp at one or both of the foci of the ellipse.
|

