HYPERBOLA : Caustic curves
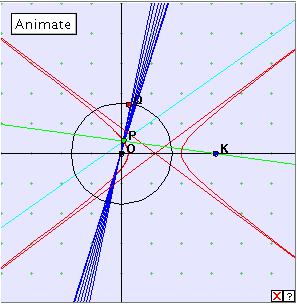
 Because of the close relationship between the hyperbola and the ellipse, we might expect the caustic curves of the hyperbola to be similar to the those of the ellipse. As usual, we take the line from point K to general point P on the hyperbola, and then reflect this line in the normal to the curve at P. The envelope of these reflected lines is the caustic of the hyperbola relative to the radiant point K. Because of the close relationship between the hyperbola and the ellipse, we might expect the caustic curves of the hyperbola to be similar to the those of the ellipse. As usual, we take the line from point K to general point P on the hyperbola, and then reflect this line in the normal to the curve at P. The envelope of these reflected lines is the caustic of the hyperbola relative to the radiant point K.
Click the linked diagram below, and then click the ‘Animate’ button to generate the caustic curve of the hyperbola with respect to the point K. Clicking the little red x which appears at bottom right will clear the drawing from the applet window. Now drag the red point Q slowly around the circle. Can you describe the construction? Experiment with different positions of the point K. Of special interest is when K lies at the centre of the hyperbola, when K lies at a focus of the hyperbola, and when K is ‘at infinity’. (Drag the point K right along the x-axis to the edge of your monitor. Refresh the window to later retrieve K.)
Some of the caustic curves here appear to be hyperbolic in shape with a cusp or two at the foci of the ellipse. I notice that the MathWorld site refrains from venturing an opinion on these curves. If you can identify these caustic curves, I am reminded of the Kipling line ‘You're a better man than I am, Gunga Din!’
|
 Because of the close relationship between the hyperbola and the ellipse, we might expect the caustic curves of the hyperbola to be similar to the those of the ellipse. As usual, we take the line from point K to general point P on the hyperbola, and then reflect this line in the normal to the curve at P. The envelope of these reflected lines is the caustic of the hyperbola relative to the radiant point K.
Because of the close relationship between the hyperbola and the ellipse, we might expect the caustic curves of the hyperbola to be similar to the those of the ellipse. As usual, we take the line from point K to general point P on the hyperbola, and then reflect this line in the normal to the curve at P. The envelope of these reflected lines is the caustic of the hyperbola relative to the radiant point K.