|
CYCLOID : Generation
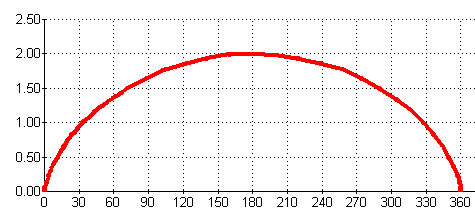
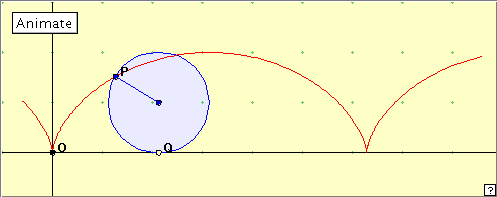
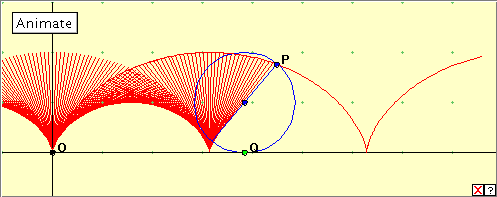
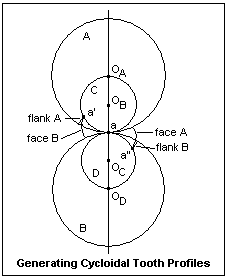
The cycloid has a long history, and it is not always easy to differentiate between fact and fiction. Galileo attempted to find the area, Roberval and Christopher Wren succeeded in finding the length of (a branch of) the curve, and in 1658 Blaise Pascal offered a prize for the solution of various problems connected with ‘la Roulette’ as it was called by the French. Generation as a locus The applet below generates the cycloid. This is the traditional construction based on the trajectory of a point on a rolling circle. Click the linked figure below, and then click the 'Animate' button to generate the cycloid. Click the button again to stop the generation. You can also see the construction more slowly by manually dragging the green point Q. Do you understand the construction? We notice that the driving point Q is not directly below P as would happen if its coordinate was the x-coordinate of P. This is because the coordinate of Q has been chosen as the parameter in the parametric equations of the cycloid. We explore this later under ‘Exploration’. Generation as an envelope We can picture the generation of the cycloid as an envelope by making a simple modification of the above applet. We simple extend the radius through P to become a diameter of the circle. As the circle rotates, this diameter generates a cycloid half the size of the original. Click the figure below to open the linked applet. Now click the ‘Animate’ button. What do you notice about the diameter through P? Why is the generated cycloid half the size of the original? Remember, clicking the little red cross at bottom right will delete the traced red figure. Experiment with manually moving the green point Q. We can see that the generated cycloid is half the size of the original by noting that Reflection The construction of an applet for generating the cycloid raises some interesting questions. There is no programming way of making a circle ‘roll’ along a line, so we imply the rolling motion by the use of the fixed point P and the radius of the circle. OCCURRENCES The cycloid occurs as the curve generated by a point on a rolling circle. It also occurs as the solution of the Tautochrone and Brachystochrone Properties – properties relating to the behaviour of particles sliding down curved paths.Apart from these, real life occurrences are fairly rare. The curve occurs in connection with certain gearing arrangements, the so-called cycloid pinwheel, and also in connection with a certain type of fish scale (see pictures below).
|