DELTOID : Exploration

The deltoid has parametric equations

x = 2a cos t + a cos 2t, y = 2a sin t – a sin 2t where 0 t < 2.

We can see from these equations that when t = 0, x = 3a, and when t = , x = – a. So the deltoid has an intercept of 4a on the x -axis. In fact, the origin is the centre of the inscribed circle (see right) which has radius a.

Setting a = 1, the Cartesian equation of the deltoid turns out to be the rather unpleasant

(x2 + y2)2 + 18(x2 + y2) = 8x3 – 24y2x + 27.

This equation describes the deltoid with cusps at t = 0°, 120° and 240°.

It is known that the area of the deltoid is A = 2 a2, and the length is L = 16a.


A family?

At this point there seems to be a question requiring an answer. Are the deltoid and the astroid members of a family of curves for which we might describe a general member? Suppose we take three equally angled rays from the origin and link them with some inward curving arcs (to be properly defined), we obtain the deltoid. If we do the same thing with four rays from the origin, we obtain the astroid. Why not take n equally angled rays?

Unfortunately, there is little common pattern to be seen in either the parametric equations, or the Cartesian equations of the two curves. Perhaps the answer to this question will become clearer as we continue our investigations. However, a family resemblance would be confirmed if the deltoid had analogous properties to the astroid. Let us see!

The curve and parameter

The deltoid with a = 1, is generated by the linked applet at right.

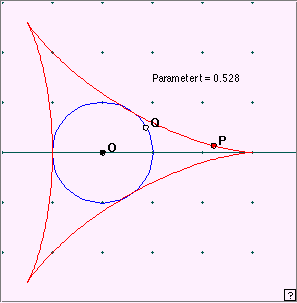
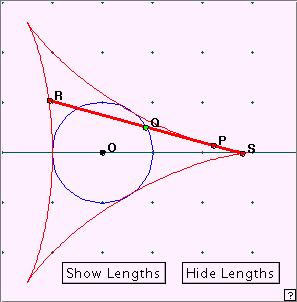
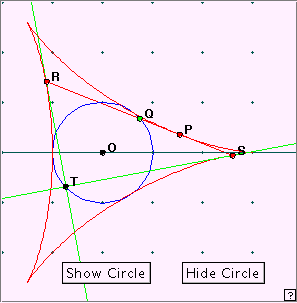
Move point P by manually shifting the driving point Q around the circle. The actual values of t are given below the scale. Notice that the curve has three cusps. For what (exact) values of t are these obtained? What distance is the origin from each cusp? from each opposite curved edge?

Remember that in this case the curve is being defined parametrically, not in polar coordinates. Hence, perhaps surprisingly, the points O, Q and P are not always collinear. In fact they are collinear in just six positions: at the cusps and at the touching points of the deltoid with the incircle. Although the numerical values of t are given, you can correctly guess that for this placing of the deltoid, the cusps are obtained for t = 0, 2 /3, and 4 /3. Noting the marked coordinate points, we see that the origin O is 3 units from each cusp, and 1 unit from each opposite curved edge (in general, 3a and a).

Length of tangent segment

The first astroid property we looked at concerned the length of a tangent to the curve, cut off by the axes. It is easily seen that nothing like this works for the deltoid, whether we take the axes, or three equally spaced rays from the origin. But there is an interesting tangent property.

Look at the applet linked at right. As above, you can move the point P around the deltoid by manually moving the point Q. At each point P on the deltoid we have drawn the tangent – in fact a segment of the tangent line cut off by the two further intercepts with the deltoid curve. Can you make a conjecture about the length of this tangent segment? What about the point Q where this moving segment meets the incircle?

Now click the ‘Show lengths’ button. What do you find?

Notice that in this construction we have chosen a = 1 (as indicated by the coordinate points in the figure), but we have left the length measurement in pixels: 100 pixels = 1 unit.

We conjecture the:

Theorem The tangent at any point P of a deltoid is intercepted again by the deltoid curve determining a segment of constant length 4a. The midpoint of this segment lies on the incircle of the deltoid.

[Programming note: I always intended writing this program ‘backwards’ using the final result. So: construct the tangent at P, choose a point M where the tangent meets the incircle, and then construct intercepts R and S on the tangent line distant 2 from the (assumed) midpoint M. This construction idea ran into trouble because choosing the point M made use of the command Intersect1 or intersect2 – sometimes one, and sometimes the other! Then I discovered that by some miracle, the point Q which was being used to drive the parametric drawing of the deltoid, turned out to be the actual midpoint. There is some mathematics hidden here, but I’m not sure what it is ... .]

Perpendicular tangents

In the figure at right we show our previous construction of a tangent (segment) RS at point P of the deltoid. We now construct tangents to the deltoid at the two endpoints R and S.

Play with the applet linked at right. As before, the green point Q slides to move P around the deltoid. What appears to be true about the green tangents at R and S? Can you make two observations? Given the (programming) difficulty of constructing the two tangents, can you suggest a method of finding the point of intersection T? Now click the ‘Show Circle’ button.

It appears that the two green tangents meet at right angles on the incircle. Assuming this to be correct, we could locate T by considering where the circle on RS as diameter meets the incircle. Now comes a surprise: this circle appears to actually touch the incircle. This probably explains the slightly ‘delicate’ nature of this applet: the point T is intermittently undefined as the approximate pixelated circles fail to have an actual point in common.

Perpendicular tangents and normals

We can carry this process one step further by adding the normals to the tangents at the points R and S.

Play with the linked applet at right. What is the large blue circle? The normals to the tangents at R and S are RN and SN. What can you say about the point N? Click the ‘Show Circle’ button. What do you notice? How is the yellow rectangle constructed? Are you sure it is a rectangle? Is the rectangle ever a square? When?

The large blue circle is the circumcircle of the deltoid – the smallest circle which contains this curve. The applet gives us a very strong conjecture that the normals at R and S meet at a point N on this circumcircle. If we add in the circle on RS as diameter, we again get a very strong indication that this circle touches the circumcircle at the point N.

This figure contains such a lot of interesting mathematics! The yellow rectangle is an artistic touch. It is of course a rectangle, since the normals are perpendicular to the tangents, which also meet at right angles. The rectangle appears to be a square when point P lies at the points of contact of the deltoid and the incircle. A little calculus will show you that the area of this rectangle varies between a maximum of 8 (when the rectangle is square) and a minimum of 0 (where is this value taken?).

Our work so far indicates that despite apparent similarities, the deltoid and the astroid behave in quite different ways.



Bibliography

A Book of Curves, Lockhart, E. H. (C.U.P. 1967)