|
DELTOID : Generation
The deltoid was first considered by Euler in 1745 in connection with an optical problem. It was later considered by Jakob Steiner in 1856. The following construction is a little sophisticated, but it does result in the deltoid being generated as an envelope of straight lines. Steiner discovered that the deltoid occurred as the envelope of the Simson lines of a triangle. You may like to read more about the Simson line. For example, see: http://homepage.mac.com/paulscott.info/PLC/5/5.html
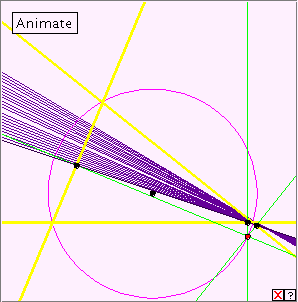
The applet below generates the deltoid by Steiner’s method. Click the linked figure below, and then click the ‘Animate’ button to generate the deltoid. Click the button again to stop the generation. Clicking the little x at bottom right will clear the drawing from the applet window. Now slowly drag the red point around the circle. Can you see how the construction works?  This applet is rather more complicated than previous ones. Click the x box of the applet to clear the window. Can you find the point on the circumcircle? the three perpendiculars to the sides of the triangle? the Simson line? Notice how that when the point is moved around the circumcircle, the feet of the perpendiculars remain collinear. Even this is pretty amazing! And the Simson line generates a deltoid ... . Reflection The sinilarites between the deltoid and the astroid would seem to suggest that they belong to the same family of curves.
|
The name ‘deltoid’ for this curve comes from its similarity in shape to the Greek letter delta 
. It is sometimes called a tricuspoid because of its three cusps.
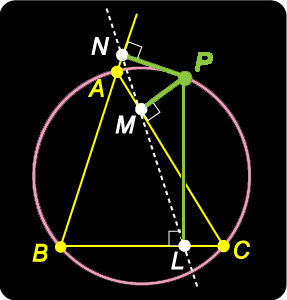However, it will be enough for our purposes here to observe that the Simson line of a triangle is the line through the feet of the perpendiculars to the sides of the triange from a point on the circumcircle of the triangle. So in the figure at right, LMN is the Simson line of point P on the circumcircle of triangle ABC.
