|
ELLIPSE : Generation
The applet below generates the ellipse. Click the linked diagram below, and then click the ‘Animate’ button to generate the ellipse. Click the button again to stop the generation. Clicking the little red x which appears at bottom right will clear the drawing from the applet window. Now drag the red point slowly around the circle. Can you describe the construction? Reflection This method of generating the ellipse creates an envelope of lines, thus determining the shape. This is the dual of creating a shape as a locus of points. Through each point P on the (circum-)circle, we draw the line perpendicular to PF. The ellipse occurs as the envelope of these lines. The central symmetry of the ellipse might suggest the existence of another point F' on the horizontal line through C, with FC = CF'. Our construction would work equally well using this new point. Each of F, F' is called a focus of the ellipse (plural foci, pronounced to rhyme with ‘low sigh’). We have not established that the curve obtained here is actually an ellipse. The proof, which is not trivial, can be found in Lockwood’s excellent book A Book of Curves. Occurrences Let us look at some of the places the ellipse occurs in real life. Many of these arise as in our first introduction, by viewing a circular image at an angle. We see this in the examples below: the circular bicycle wheels, the circular bell of the tuba, and the spotlight image, where the conical ray of light is sliced through at an angle by the stage.
An even more direct example is the Tycho Brahe Planetarium in Copenhagen, shown below left. This cylindrical building was designed bye the Danish architect Knud Munk. If you looked straight down on it from above, it would appear circular. However the roof is elliptical in shape because of the angle. Sometimes shapes are elliptical because they are constructed that way, as with the oval in Washington DC shown below centre.
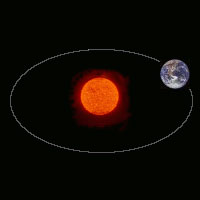
And finally, around 1605, Johannes Kepler discovered that the planets move around the sun in elliptical orbits, a finding which revolutionized the astronomy and physics of the time. This is illustrated above right.
|
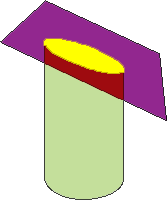 The ellipse is one of the so-called conic sections : it can be obtained as the cross section of a right circular cone when intersected by a plane. We notice from the diagram at left that the ellipse also occurs as a section of a circular cylinder. In fact, we can think of the cylinder as a special type of circular cone in which the vertex is ‘at infinity’. The ellipse was first studied as a conic section by the early Greeks. It is an example of a central conic: there is a point, the centre, which bisects all chords of the ellipse passing through it. We can also think of the ellipse as a projection of a circle, or the circle as a special type of ellipse, where the intersecting plane is perpendicular to the axis of the cylinder or cone.
The ellipse is one of the so-called conic sections : it can be obtained as the cross section of a right circular cone when intersected by a plane. We notice from the diagram at left that the ellipse also occurs as a section of a circular cylinder. In fact, we can think of the cylinder as a special type of circular cone in which the vertex is ‘at infinity’. The ellipse was first studied as a conic section by the early Greeks. It is an example of a central conic: there is a point, the centre, which bisects all chords of the ellipse passing through it. We can also think of the ellipse as a projection of a circle, or the circle as a special type of ellipse, where the intersecting plane is perpendicular to the axis of the cylinder or cone.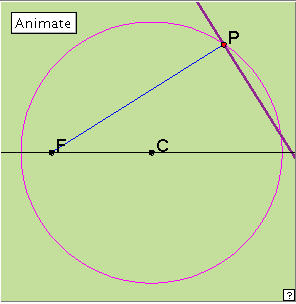





 If an ellipse is rotated about its major axis, it generates a solid ellipsoid. The common football gives a close approximation to this.
If an ellipse is rotated about its major axis, it generates a solid ellipsoid. The common football gives a close approximation to this.