EVOLUTE

In this section we give java applets which generate the evolutes of each of our curves.

The evolute of a curve can be defined in two different, but equivalent ways.

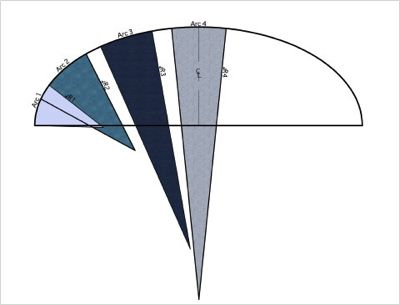• As a locus. Each portion of a (non-straight) curve can be closely approximated by an arc of a circle. Hence at each point of such a curve, there is an associated circle of curvature, with a corresponding radius of curvature and centre of curvature.

The evolute of the curve can be defined as the locus of these centres of curvature.

• As an envelope. An easier definition is to define the normal at each point of the given curve. This is the line which is perpendicular to the tangent (touch line) at each point of the curve.

The evolute is the envelope of these normals.

These two definitions are equivalent. For strictly, we would obtain the centre of curvature C associated with a point Q of the curve as the limit of the intersection of two normals at points approaching Q on the curve. Similarly, the normals are tangents to the evolute envelope. As two such normals approach coincidence, their limiting position C is a point on the envelope.

The original curve is called the involute of the newly constructed curve.

You might like to think about whether you would expect the evolute of an evolute to be the involute of the first evolute!

Or, if this wasn’t true, perhaps we could obtain a whole sequence of evolutes? And would the curves in this sequence approach some limiting curve? Or might there be some cycle of curves, each the evolute of the preceding one? There is obviously some room for investigation here!

We shall use the second envelope method for constructing evolutes with our JSP programming.


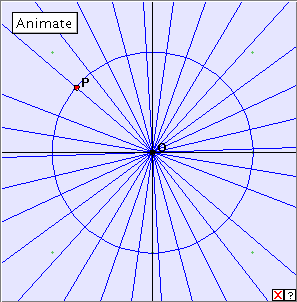There is one practical problem which occurs frequently with our evolute constructions. We can illustrate this by finding the evolute of a circle. In theory, it is clear that the normals of a circle all meet at the centre. That is, the evolute of the circle is a point, the centre. Now how do we illustrate this using JSP? If we draw in all the normals, we cover the whole plane which is not helpful. However, if we just draw in a selected few of the normals, the result is clear. In JSP we can do this using the designated bracketed number in this sample command:

AnimateButton(10, 10, 'Animate', 9, 8) (10) (1) (1);

If this number is 1 or 2, we obtain many normals; higher values such as 10 result in fewer normals being drawn.



Bibliography


A book of curves, Lockwood, E. H. (Cambridge University Press 1967).

Rather mathematical but with examples: http://mathworld.wolfram.com/Evolute.html