|
 Because of the close relationship between the hyperbola and the ellipse, we might expect the evolute of the hyperbola to be similar to the evolute of the ellipse, and it turns out that this is indeed the case. As usual, we think of the hyperbola as a locus of points, and construct the normals to these points. The evolute occurs as the envelope of these normals. Because of the close relationship between the hyperbola and the ellipse, we might expect the evolute of the hyperbola to be similar to the evolute of the ellipse, and it turns out that this is indeed the case. As usual, we think of the hyperbola as a locus of points, and construct the normals to these points. The evolute occurs as the envelope of these normals.
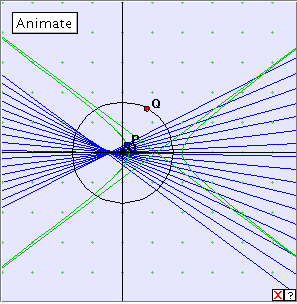
Click the linked diagram below, and then click the ‘Animate’ button to generate the evolute of the hyperbola with respect to the centre of the hyperbola (O). Clicking the little red x which appears at bottom right will clear the drawing from the applet window. Now drag the red point Q slowly along the x-axis. Can you describe the construction? Do you recognize the evolute?
Notice that the locus construction generates both branches of the hyperbola. For each of these we obtain an evolute curve which is virtually the same as the Lamé curve obtained for the ellipse.
The Cartesian equation for the evolute is
From a point between the two branches of the evolute, two normals can be drawn to the hyperbola. However, from a point beyond the evolute, four normals can be drawn.
|
 Because of the close relationship between the hyperbola and the ellipse, we might expect the evolute of the hyperbola to be similar to the evolute of the ellipse, and it turns out that this is indeed the case. As usual, we think of the hyperbola as a locus of points, and construct the normals to these points. The evolute occurs as the envelope of these normals.
Because of the close relationship between the hyperbola and the ellipse, we might expect the evolute of the hyperbola to be similar to the evolute of the ellipse, and it turns out that this is indeed the case. As usual, we think of the hyperbola as a locus of points, and construct the normals to these points. The evolute occurs as the envelope of these normals.