Because there is a whole family of limaçons, the problem of finding the evolute becomes much more interesting. The cardioid occurs as a special case (when sliding point K lies at C ), and the evolute is easily recognizable here as a cardioid one third the size of the original. But what happens for other positions of the sliding point K ?

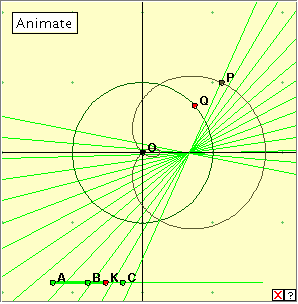
Click the diagram below to open the applet, and then click the ‘Animate’ button to generate the evolute of the limaçon. Clicking the little red x at bottom right will clear the drawing from the applet window. Now drag the red point Q slowly around the circle. Can you describe the construction? Moving the point K along the horizontal line will change the shape of the limaçon, and hence the inverse curve. See if you can classify the evolutes according to the position of point K. Some of them look pretty strange!