hyperbola : exploration

Hyperbola : Exploration

Properties

When the hyperbola is studied analytically, it is the locus of points (x, y) in the plane which satisfy the equation

.

We notice that the equation is exactly the same as the equation for the ellipse except for a change in sign. We should therefore not be too surprised if we find that the properties of the hyperbola and the ellipse are fairly similar. We associate with the hyperbola two points F and F' (the foci) on the x-axis, and two lines d and d' (the directrices) perpendicular to the x-axis. The foci are equidistant from the origin, as are the directrices, and the actual distances are determined by the hyperbola. The hyperbola is symmetric about the origin which is called the centre of the hyperbola.

From the equation, we see that the hyperbola cuts the x-axis in the points (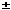a, 0), and does not cut the y-axis in any real points. If we write e = b/a, the number e (> 1) is called the eccentricity of the hyperbola. Now the foci have coordinates ( 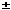ae, 0), and the directrices meet the x-axis in the points ( 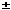a/e, 0). This is the same as for the ellipse, but the different range for e changes the order of the x-intercepts.

We observe that the points of the hyperbola lie on two distinct branches. It is possible to draw through the origin two intersecting diagonal lines which are ‘tangent at infinity‘ to these branches; these are called the asymptotes to the curve. If these two asymptotes intersect at right angles, the hyperbola is called a rectangular hyperbola.


Let us now investigate some interesting properties of the hyperbola.



Focus-directrix property

The adjacent diagram shows an applet of a hyperbola with its foci and directrices. Click the diagram to open the applet, and then click the ‘Animate’ button and watch what happens. Now stop the animation (click the button again), and try various positions of P by manually dragging the point P along the x-axis.

Try measuring the distances of the point P from a focus and the corresponding directrix for a number of positions of P. What can you say about the ratios of the distances? What is the eccentricity of this hyperbola? State the property that you see illustrated here.

We have illustrated here a basic property of the hyperbola: a hyperbola is the locus of points which are in constant ratio e (> 1) from a fixed point (focus) and a fixed line (directrix).







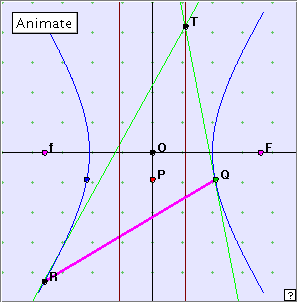Focal chord property

Now look at this next applet. As usual, click the diagram to open the applet. QR is a chord through the focus F – a focal chord of the hyperbola (notice the line QR passes through F). We have drawn tangents at the ends of the focal chord.

What do you notice about the tangents? What appears to be true about segments TF and QR?

We see that the tangents at the end of a focal chord meet at a point T on the corresponding directrix. Further, the segment FT is perpendicular to the focal chord. This applet is interesting in that the focal chord switches from having an endpoint on each branch, to having two endpoints on the right branch. It is almost as though the hyperbola ‘wraps around behind’ so that the branches join.

[Programming note The note for the corresponding ellipse applet also applies here.]




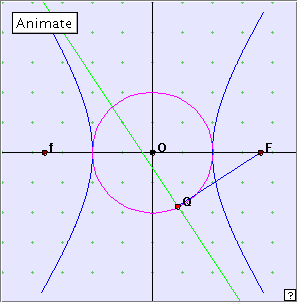An envelope property

In the diagram at right, we have shown a circle which has radius a centred at the origin, and passing through the intercept points of the hyperbola with the x-axis. This is called the auxiliary circle of the hyperbola. Now run the applet, using both the ‘Animate’ button and manually.

Describe what is happening here. How would you define the line which is generating the hyperbola?

This is an easy way to generate the hyperbola. Choosing any point Q on the auxiliary circle, and focus f, the line through Q perpendicular to Qf is tangent to the ellipse. Think about what happens when we choose the other focus F.









Focal distance sum property

The hyperbola is often defined in the following way. Given two points F and F', the locus of points Q for which F'Q – QF = constant is a hyperbola. Can we illustrate this dynamically? Check out the adjacent applet, using the ‘Animate’ button, and moving point P manually along the x-axis.

We are looking at the difference of the lengths, fQ – FQ. What length is equal to FQ? What length is equal to the difference fQ – FQ? If this sum is constant, what would you expect the locus of T to be? Is it?!

Since F and T both lie on the same (variable) circle centre Q, we have QF = QT, Hence fQ – QF = fQ – QT. If this is constant we expect the locus of the variable point T to be a circle centre f. This result is illustrated by the applet.

Could we change the roles of f and F here?






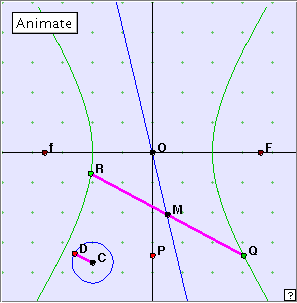The parallel chords property

We found that the midpoints of parallel chords of an ellipse lie on a straight line through the centre of the ellipse. We might expect a similar behaviour with the hyperbola.

Open the applet. You can choose the direction of the chords using the little indicator dial at bottom left. Now click the ‘Animate’ button, or manually move the point P.

Notice the locus of the point M which is the midpoint of chord PQ. Describe this locus. What name would you suggest for it? For any fixed position of the chord, where do you think the tangents at Q, R might meet?

The locus of the midpoints of parallel chords of a hyperbola is a straight line through the centre of the hyperbola. This line is called a diameter of the diameter. The tangents at the end of any such chord meet on the corresponding diameter.





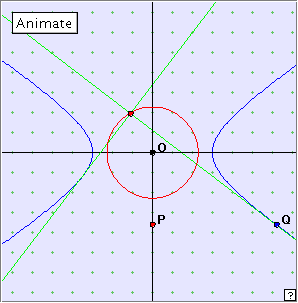The perpendicular tangent property

For this property we need to change the defining parameters for the hyperbola to make it ‘flatter’. Otherwise we won‘t find any perpendicular tangents at all!

Open the applet at right, and experiment using the ‘Animate‘ button, and manually moving the point P.

The green line through Q is the tangent. The other green line is also a tangent to the hyperbola. How are these two tangents related? What is the locus of their point of intersection? Given that in the equation of this hyperbola we have taken a = 3 and b = 2, can you suggest a radius for the given circle?

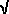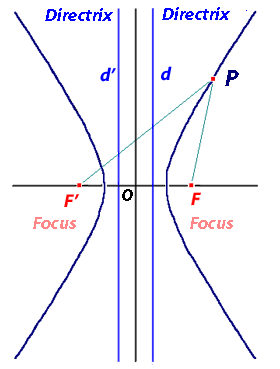
The red circle is called the director circle of the hyperbola. It occurs as the locus of the point of intersection of perpendicular tangents to the hyperbola. It has radius (a2 – b2) = 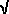5 in this case. Notice that the director circle only exists for a > b. Can you relate this to the shape of the hyperbola? (Think about when the perpendicular tangents will exist.)


Bibliography