|
HYPERBOLA : Generation
The applet below generates the hyperbola. It differs from the applet for the ellipse only in that the generating circle has been chosen smaller, and the point F lies outside the circle, rather than interior to it. Click the linked figure below, and then click ‘Animate’ button to generate the hyperbola. Click the button again to stop the generation. Clicking the little red x at bottom right will clear the drawing from the applet window. Now drag the red point slowly around the circle. Can you describe the construction? Here is another exercise. While dragging the red point slowly around the circle, you will notice that there are two generating lines which pass through the centre C. These two lines are called the asymptotes of the hyperbola. As we move a point further and further out on either of the branches of the hyperbola, that point moves closer and closer to the corresponding asymptote. In fact we can think of each asymptote as being ‘tangent to the hyperbola at infinity’. Reflection This method of generating the hyperbola creates an envelope of lines, thus determining the shape. The central symmetry of the hyperbola might suggest the existence of another point F' on the horizontal line through C, with FC = CF'. Our construction would work equally well using this new point. Each of F, F' is called a focus of the hyperbola. We have not established that the curve obtained here is actually an hyperbola. As for the ellipse, the proof, which is not trivial, can be found in Lockwood’s excellent book A Book of Curves. Occurrences Let us look at some of the places the hyperbola occurs in real life. There is an obvious occurrence corresponding to the definition of the hyperbola as a section of a cone. This is illustrated below left , where the ray of light from the torch forms a hyperbolic shape on the wall.
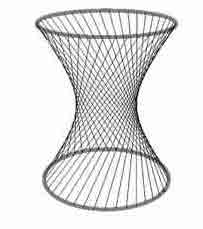
If we take a hyperbola and rotate it about the vertical axis (using the orientation we have adopted on this page) we generate a solid called a hyperboloid of one sheet. This is a very graceful shape, and is of mathematical interest because although the surface is curved, it can be generated by two intersecting sets of straight lines. This is illustrated above right. Olden days wastepaper baskets were often constructed in the shape, with straight lengths of wire forming the generators.
The hyperbola also occurs in conjunction with the parabola as a cross-section of the hyperbolic paraboloid. This is another nice shape which is sometimes seen in roof lines. An example is the entrance to the Wave Garden in Louisville, shown below.
|
 The hyperbola is one of the so-called conic sections : it can be obtained as the cross section of a right circular cone when intersected by a plane which is parallel to the axis of the cone. We notice from the diagram at left that if such a plane passes through the vertex of the cone, we obtain a line pair. Thus a line pair can be thought of as a degenerate hyperbola. The hyperbola was first studied as a conic section by the early Greeks. It is an example of a central conic: there is a point, the centre, which bisects all chords of the ellipse passing through it.
The hyperbola is one of the so-called conic sections : it can be obtained as the cross section of a right circular cone when intersected by a plane which is parallel to the axis of the cone. We notice from the diagram at left that if such a plane passes through the vertex of the cone, we obtain a line pair. Thus a line pair can be thought of as a degenerate hyperbola. The hyperbola was first studied as a conic section by the early Greeks. It is an example of a central conic: there is a point, the centre, which bisects all chords of the ellipse passing through it. 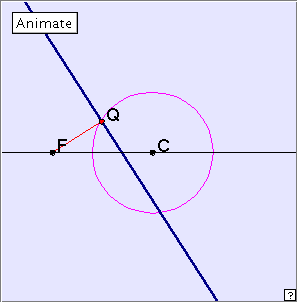
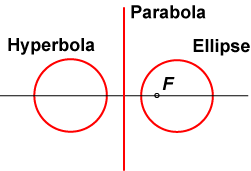 However, the pattern is revealed in a different way. In the adjacent figure, we have shown a focus F. The circle at right represents the base circle for the construction of an ellipse. Now think of taking this circle larger and larger until in the limit it becomes a straight line. Together with F, we can use this to generate the parabola. Now think of this line bending back on itself to become a circle, and so obtaining the circle on the left. Together with F, this represents the base circle used for constructing the hyperbola.
However, the pattern is revealed in a different way. In the adjacent figure, we have shown a focus F. The circle at right represents the base circle for the construction of an ellipse. Now think of taking this circle larger and larger until in the limit it becomes a straight line. Together with F, we can use this to generate the parabola. Now think of this line bending back on itself to become a circle, and so obtaining the circle on the left. Together with F, this represents the base circle used for constructing the hyperbola.