|
CATENARY : Inversion
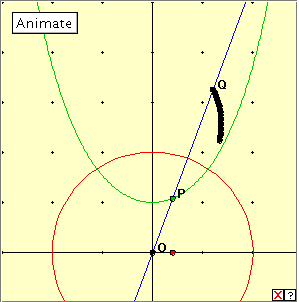
Click the diagram below to activate the applet, and then click the ‘Animate’ button, or manually drag the red driver point along the x-axis. Notice that points P and Q are inverse with respect to the fixed red circle. Point P traces out the catenary, point Q traces out the inverse curve. How would you describe the inverse curve? Is it a curve that we have discussed already? |
 We begin with our catenary locus, derived as before as the average of two exponential functions. In taking the inverse of this curve, an obvious choice for the centre of inversion is the given origin.
We begin with our catenary locus, derived as before as the average of two exponential functions. In taking the inverse of this curve, an obvious choice for the centre of inversion is the given origin.