|
HYPERBOLA : Inversion
Because the equation of the hyperbola is so similar to the equation of the ellipse, we follow the pattern of construction used there, using the Cartesian equation in the first applet, and the polar form in the second.
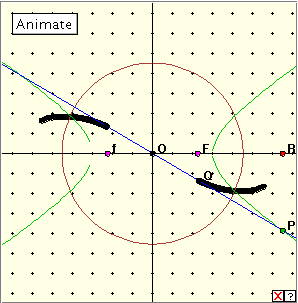
where we have taken a = 3 and b = 2. The driver point here moves along the x-axis. In fact, this method is not ideal in at least two respects. Firstly we have to construct the hyperbola in two parts: the upper and lower portions. And secondly, the hyperbola may not be well drawn near the x-axis where the curve is near vertical. In the second case we have used the polar form using one of the foci as the ‘pole’. This generates the hyperbola nicely, but as with the ellipse, there are questions in the programming as to exactly where the origin then lies!
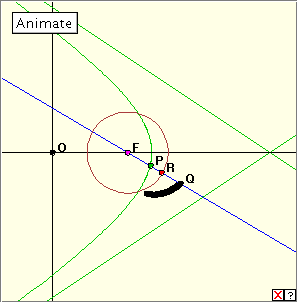
Let us then take a circle of inversion with centre at the origin. As usual, the radius chosen for the circle of inversion is not important here. Because the hyperbolic locus is constructed in two parts here – upper and lower – we have taken the inverse of the lower half and reflected it in the origin. The resulting inverse curve is a relative of the lemniscate which we have seen before. Notice that since the points of the lemniscate near the origin correspond to points of the hyperbola a great distance away, we have to allow the point R to travel a fair distance out along the x-axis. When the hyperbola is a rectangular hyperbola (that is, the asymptotes are perpendicular) it is easy to see that we get the standard lemniscate. For the polar coordinates in this case are: Rectangular Hyperbola : r2 = 1/(cos 2 Obviously the product of these two r-values is always constant. We get another interesting result when we take the centre of inversion as one of the foci of the hyperbola. The hyperbola below was constructed using polar coordinates, taking F as the pole. This avoids the problem in the above applet of the hyperbola appearing as the union of two halves. In the diagram below we have used the (red) circle of inversion as the construction circle of the ellipse. Click the linked diagram below, and then click the ‘Animate’ button to generate the inverse of the ellipse with respect to the focus F. Click the button again to stop the generation. Clicking the little red x which appears at bottom right will clear the drawing from the applet window. Now drag the red point R slowly around the circle. Can you describe the construction? Do you recognize the inverse curve? The inverse curve here is in general a limaçon, of which the cardioid is a special case. When the asymptotes of the hyperbola meet at an angle of 60°, the inverse curve is the trisectrix. It is easy to see why we might expect the limaçon here. The polar equations are: Hyperbola : l/r = 1 + e cos Limaçon : r = k + 2a cos Bibliography Ellipse inversion video : http://video.aol.com/video-detail/hyperbola-vertex-inverse/2840721831
|
 We have seen how the ellipse occurs as a centrally symmetric curve with centre at the origin O, and two other special points F and F' known as the foci. So obviously if we are interested in finding curves inverse to the ellipse, we would consider circles of inversion at these special points. By symmetry it is clearly immaterial which focus we choose.
We have seen how the ellipse occurs as a centrally symmetric curve with centre at the origin O, and two other special points F and F' known as the foci. So obviously if we are interested in finding curves inverse to the ellipse, we would consider circles of inversion at these special points. By symmetry it is clearly immaterial which focus we choose.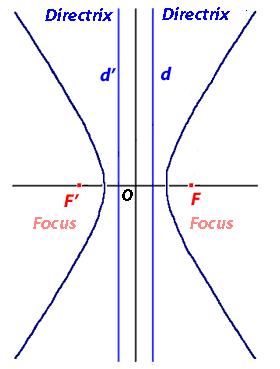 In the first case we use the Cartesian form of the equation
In the first case we use the Cartesian form of the equation