|
INVERSION
In this section we give java applets which generate the inverse of each of our curves – or at least, those inverses which are interesting. In some cases this will give us a new relationship between existing curves that we have discussed. In other cases we will get some new curve which may or may not be ‘interesting’! Clearly points P, P' are inverse to each other, as are the curves K, K'. The points lying on the circle of inversion are their own inverses. Points inside the circle of inversion map to points outside the circle of inversion, and conversely. Inversion is a useful tool, particularly in that branch of geometry known as projective geometry. A number of properties of inversion are known, the main ones being: • a straight line through the origin maps to a straight line through the origin (the same line in fact); • a straight line not through the origin maps to a circle through the origin; • a circle through the origin maps to a straight line not through the origin; • a circle not through the origin maps to a circle not through the origin; • angles between curves are preserved under inversion. For proofs of these properties you might like to look at (for example): http://homepage.mac.com/paulscott.info/PLC/12/12.html
However, we observe that when taking the inverse of a general curve, the size of the circle of inversion is not important (apart from the placing of the image in our applet window). However, the choice of centre is important: a different centre may well result in a different inverse image curve. |
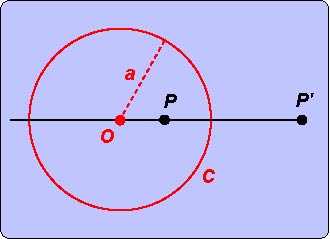 But first let us describe the transformation known as inversion.
But first let us describe the transformation known as inversion.