|
LEMNISCATE : Inversion
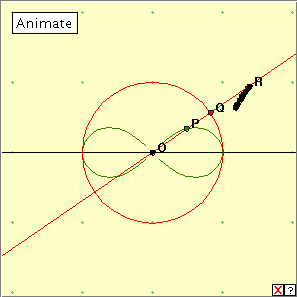
In the applet linked below, as Q traverses the red circle, point P describes the lemniscate. Point R is the inverse of P with respect to the red inversion circle. Press the ‘Animate’ button to see the locus of R. You can delete this locus by clicking on the red cross at lower right. A fuller representation of the locus can be found by manually dragging the point Q around the red circle. What is the locus of R? Is this a curve we have seen before?
The inverse curve here is a rectangular hyperbola with centre at the origin O. This is a hyperbola for which the diagonal asymptotes are at right angles. We expect this result. For the polar coordinates in this case are: Lemniscate : r2 = a 2 cos 2 Rectangular Hyperbola : r2 = 1/(cos 2 Obviously the product of these two r-values is always constant.
Bibliography
|
At left is a picture of the lemniscate – the ‘ribbon curve’. The leniscate has an obvious central point which we will take as our centre of inversion. As usual the radius of the inversion circle is not important: we choose the circumcircle of the lemniscate as our circle of inversion.
.