|
LIMAÇON : Inversion
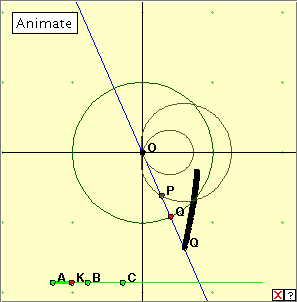
Click the diagram below to open the applet, and then click the ‘Animate’ button to generate the inverse of the limaçon. Click the button again to stop the generation. Clicking the little red x at bottom right will clear the drawing from the applet window. Now drag the red point slowly around the circle. Can you describe the construction? Moving the point K along the horizontal line will change the shape of the limaçon, and hence the inverse curve. See if you can classify the inverse curves according to the position of point K. When K lies at point A the limaçon degenerates to a circle through O. The applet actually fails here, but taking K very close to A, we observe that the inverse curve is the vertical tangent to the circle where it cuts the x-axis, as expected. For K lying between A and C , the inverse of the limaçon is a hyperbola. When K lies at C the limacon becomes a cardioid, and the inverse curve is a parabola. We have seen previously how the parabola ‘lies between’ the hyperbolas and the ellipses. For K lying to the right of C, the inverse curves are ellipses. Why is this so? In simple terms, the limaçon has polar equation r = k + cos Bibliography Wikipedia: http://en.wikipedia.org/wiki/Limacon
|
 We know that the cardioid is a special curve in the family of limaçcons. If you have already looked at the case of the inverse of the cardioid, then you might have some idea of what to expect here. The obvious choice for the centre of i
We know that the cardioid is a special curve in the family of limaçcons. If you have already looked at the case of the inverse of the cardioid, then you might have some idea of what to expect here. The obvious choice for the centre of i nversion here is the cusp or cross-over point for the limaçon, where that exists.
nversion here is the cusp or cross-over point for the limaçon, where that exists.