TRACTRIX : Inversion

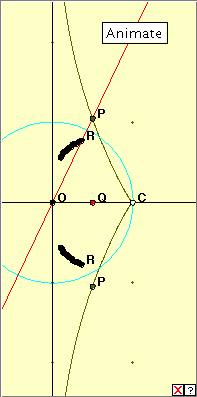
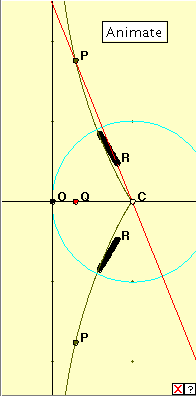
You might remember that the tractrix occurs as the path of a weight that is being pulled (in our diagram) along the y-axis. We previously drew the graph using the calculated equation, combining the upper and lower reflected arcs.

In finding the inverse, we have two obvious choices of centre of inversion: the origin which lies at the centre of the vertical straight line segment, and the cusp.

Let us first look at taking the origin as the centre.

Click on the linked diagram at right, and then click on the ‘Animate’ button. The red driver point Q moves along the horizontal x-axis, and correspondingly, the points P trace out the tractrix. The points R are the inverses of the respective points P with respect to the cyan circle of inversion. Notice the points where the tractrix and its inverse meet. What is the inverse curve? Do you recognize it?

The resulting inverse here bears some resemblance to a limaçon, but I can find no reference to this. It would appear then that this is a different, new curve.

Let us next consider what happens when the centre of inversion lies at the point C.

Click on the linked diagram below left, and then click on the ‘Animate’ button. The red driver point Q moves along the horizontal x-axis, and correspondingly, the points P trace out the tractrix. The points R are the inverses of the respective points P with respect to the cyan circle of inversion. Notice the points where the tractrix and its inverse meet. What is the inverse curve? Do you recognize it?

The resulting inverse here looks as though it might lie between a parabola and a branch of a hyperbola. However, the tractrix does not occur as an inverse of either of these curves, so this inverse curve must be a new curve for us.


Bibliography

You might like to check out the inverses of the limaçon, parabola and hyperbola in the following references.

Limaçon : http://en.wikipedia.org/wiki/Limacon

Parabola : http://mathworld.wolfram.com/ParabolaInverseCurve.html

Hyperbola : http://mathworld.wolfram.com/HyperbolaInverseCurve.html