|
LEMNISCATE : Generation
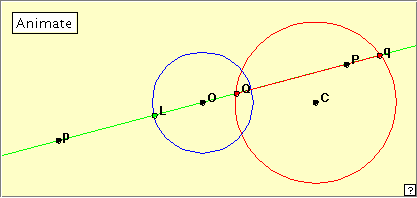
In the applet linked below, O lies outside the given red base circle. (In fact OC is 1.414 times the radius of the red circle.) A line through O meets the circle in points Q, q; its position is governed by the green driving point L. Now points P, p are chosen equidistant from O and with PO = Op = Qq. Points P, p now generate the lemniscate. As well as using the ‘Animate’ button, remember to drag the point Q manually to see what is happening here.
OCCURRENCES The lemniscate has a curious mathematical association in that it is the symbol for ‘infinity’ – a sort of displaced figure 8 which continues indefinitely. For this reason it has had some attraction as an artistic or philosophical device as illustrated below.
|
In 1694, James Bernouilli published a article on a curve ‘shaped like a figure 8, or a knot, or a bow of a ribbon’. He named this curve lemniscus which is Latin for a pendant ribbon.
