|
NEPHROID : Exploration
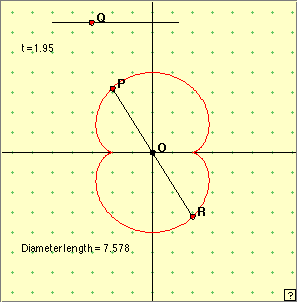
The points forming the locus of the nephroid can be defined parametrically as follows: x = a(3 cos t – cos 3t), y = a(3 sin t – sin 3t), where t varies between 0 and 2 If we wish, we can find the Cartesian coordinates of any point of the curve in this way. Finding the Cartesian equation of the nephroid is another matter, but it turns out to be (x2 + y2 – 4a2)3 = 108a4x2.
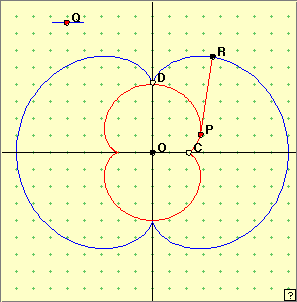
Let us take a = 1 in the above parametric equations for the nephroid. In the linked applet at right, move the point Q along the segment. Note the positions of the corresponding point P, and also the values of t. Checking with the parametric equations, can you determine the exact values of t for eight ‘special’ (and easily specified) points around the nephroid? We see from the parametric equations that the nephroid is traced out precisely when the parameter t varies by 2 Finding arc lengths of anything but the simplest curves is usually an impossible task. In the case of the nephroid, there is a surprisingly simple result. Play with the applet at right, manually moving the point Q. What value of a does the red nephroid have? the blue nephroid? In the figure, the tangent segment PR has the same length as the arc PD. Thus the arc lengths CP + PD = CP + PR. Assuming that we do obtain the blue nephroid in this way, determine the arclength CD and hence the perimeter of the whole red nephroid. For the red nephroid, a = 1; for the blue (rotated) nephroid we get twice this value. Thus the blue nephroid is twice the size of the red nephroid. In forming the tangent segment PR, we can think of peeling off, or unrolling the arc PD into a straight position along the tangent at P. Measuring C(P)R when this path lies along the x=axis gives a length of 6 = 6a. This means that the total length of the red nephroid is 24 = 24a. You might like to investigate Lockwood’s book A Book of Curves for more information on this. [There is a hidden structure in programming the point R to lie on the blue nephroid!].
A Book of Curves, Lockwood, E. H., (C.U.P. 1967). Wikipedia: http://en.wikipedia.org/wiki/Nephroid Wolfram MathWorld: http://mathworld.wolfram.com/Nephroid.html |
 Although there are a few applets which show how the nephroid is related to various other curves (we investigate these later), there are almost no applets which demonstrate intrinsic properties of the nephroid.
Although there are a few applets which show how the nephroid is related to various other curves (we investigate these later), there are almost no applets which demonstrate intrinsic properties of the nephroid.