|
NEPHROID : Generation
The applet linked to the diagram below generates the nephroid. The generation uses a fixed base circle centred at the origin, and the y-axis (or more simply, a fixed base circle and a line through the centre). Click the diagram to activate the applet, and then click the ‘Animate’ button to generate the nephroid. Click the button again to stop the generation. Clicking the little red x at bottom right will clear the drawing from the applet window. Now drag the red point slowly around the circle. Can you describe the construction? Reflection
Let Q and Q' be two points on the base circle, and let the circles with centres Q, Q' touch the y-axis at N, N'; respectively. Suppose these two circles meet again at point P. Let QQ' meet the y-axis in R. Now as Q' moves closer and closer to Q, line Q'QR becomes the tangent to the circle at Q, and the line RP becomes tangent to the nephroid at P. Further, because of the circle construction, triangles PQR and NQR are congruent. This suggests a new construction for the nephroid. For each point Q on the base circle, reflect the y-axis in the tangent to the circle at Q. The set of such image lines forms an envelope of the nephroid. Click the diagram below to activate the applet. Now click the ‘Animate’ button, or preferably move the red point manually slowly around the circle. Do you understand the constructiuon?
We set a single revolution here, because otherwise the generating lines eventually fill in the whole plane. However, the applet indicates the validity of our construction.
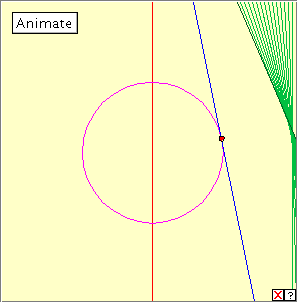
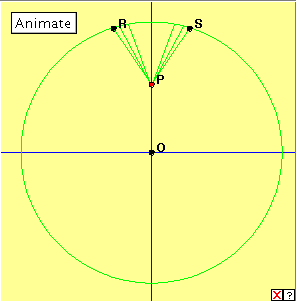
Choose two axes and a fixed base circle centred at the origin. Let P be a variable point on the y-axis. If they exist, choose points R, S on the circle such that PR = PS = PO. Use the applet below to demonstrate that segments PR, PS generate the nephroid. Click on the diagram below to activate the applet, and then click on the ‘Animate’ button, or move the red point P along the y-axis. What do you notice? In fact, the point P has to traverse the whole y-axis to generate the nephroid accurately. Occurrences The natural, real life occurrences of the nephroid are also rather rare. Just as the cardioid resembles the heart, so the nephroid roughly resembles a double kidney, but the resemblance is not close enough to be useful. The nephroid is used as the cover illustration of Lockwood's A Book of Curves and it can also occur as the ‘caustic’ light effect at the bottom of a teacup (see below).
|
 The name ‘nephroid’ means ‘kidney shaped’ and was used for this curve by English mathematician Richard Proctor in 1878 in his book The Geometry of Cycloids.
The name ‘nephroid’ means ‘kidney shaped’ and was used for this curve by English mathematician Richard Proctor in 1878 in his book The Geometry of Cycloids.
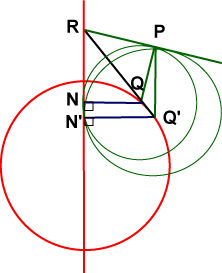 This method of generating the nephroid creates an envelope of circles, thus determining the shape.
This method of generating the nephroid creates an envelope of circles, thus determining the shape.