|
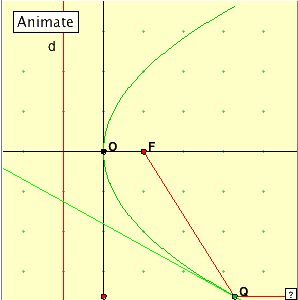
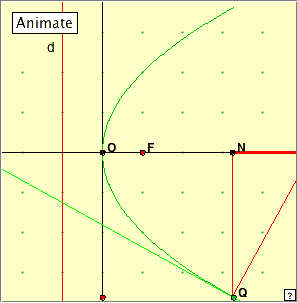
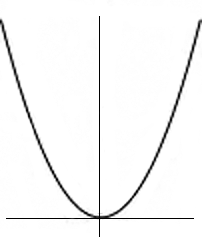
When the parabola is studied as the graph of a function, it is pictured in the ‘upright’ position as at right. This is useful for studying its properties in terms of the function State the property that you see illustrated here. If your statement involves the word ‘circle’, rephrase your statement so that this word does not occur. We have illustrated here the basic property of the parabola: a parabola is the locus of points which are equidistant from a fixed point (focus) and a fixed line (directrix). Now look at this next applet. Think of there being a light source at the focus F, and the light reflecting off the parabola. Run the animation and then manually move the point on the y-axis. What do you notice about the reflected rays? How do these lines relate to the tangent line at the point on the parabola? (You might like to use your protractor!) State a result about the parabola which is demonstrated here. This property of the parabola is the reason torches and lamps and satellite dishes have parabolic reflectors. Any light emanating from the focus, is reflected by the parabola in a direction parallel to the axis. If we draw in the tangent t at any point Q of the parabola, the angle made with t by the line QF to the focus F, is equal to the angle made by t to the line through Q parallel to the axis (‘angle of incidence = angle of reflection’).
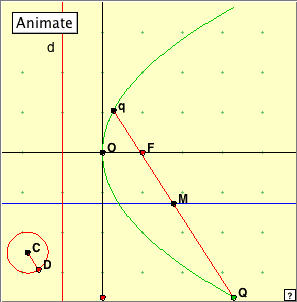
Look at the parallel chords Qq. Point M denotes the midpoint of the chord. You will notice that this point has a very nice trajectory. What is it? Look at what happens for different positions of D. For example, what is the path of M when CD is parallel to the y-axis? We see that for any set of parallel chords, the midpoints of the chords lie on a line parallel to the axis of the parabola. Click the figure at right to open the applet. This applet illustrates two interesting properties of the triangle formed by three tangents to the parabola. Click the ‘Show circumcircle ’ button. Check that it is in fact the circumcircle of Now click the ‘Show orthocentre’ button. What is the orthocentre? What rather amazing property is illustrated here? We observe two surprising results here. Firstly, the circumcentre of the triangle of tangents always passes through the focus F of the parabola. Secondly, the orthocentre of this triangle always lies on the directrix of the parabola. This makes one wonder what other surprising results lie in store for one who explores the parabola! Bibliography http://en.wikipedia.org/wiki/Parabola http://mathworld.wolfram.com/Parabola.html http://www-groups.dcs.st-and.ac.uk/~history/Curves/Parabola.html |

 Properties
Properties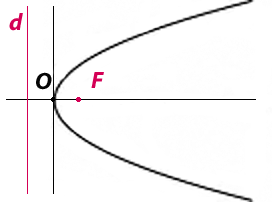 We associate with the parabola the point F (the focus) on the x-axis, and the line d (the directrix) perpendicular to the x-axis. The focus and the intercept of the directrix with the x-axis are equidistant from the origin, and the actual common distance is determined by the parabola. The x-axis here is called the axis of the parabola – the line of symmetry, and O is the vertex of the parabola.
We associate with the parabola the point F (the focus) on the x-axis, and the line d (the directrix) perpendicular to the x-axis. The focus and the intercept of the directrix with the x-axis are equidistant from the origin, and the actual common distance is determined by the parabola. The x-axis here is called the axis of the parabola – the line of symmetry, and O is the vertex of the parabola.