|
 To construct the pedal curve of the astroid relative to the origin O, we simply construct the tangents to the astroid, take the normal to each tangent from the origin, and then plot the locus of the feet of such normals To construct the pedal curve of the astroid relative to the origin O, we simply construct the tangents to the astroid, take the normal to each tangent from the origin, and then plot the locus of the feet of such normals
Click on the diagram below to open the applet, and then click on the ‘Animate’ button to generate the pedal curve of the astroid relative to the origin. Click the ‘Animate’ button again to stop the generation. Do you undertsand what is happening here? Clicking the little red x at bottom right will clear the drawing from the applet window. Now drag the red drive point Q slowly around the circle. Do you recognize the evolute of the astroid? Can you describe it? Why would you expect it to have 4-fold symmetry about the origin?
 The pedal curve of the astroid with equation The pedal curve of the astroid with equation
x = a cos3t, y = a sin3t
relative to the center O is a curve called a quadrifolium defined by the equations
x = a cos t sin2 t, y = a cos2 t sin t.
It is clear that the quadrifolium is a member of a family of rose type curves with different numbers of petals meeting at the origin.
Bibliography
Wolfram MathWorld : http://mathworld.wolfram.com/AstroidPedalCurve.html
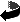
|
 To construct the pedal curve of the astroid relative to the origin O, we simply construct the tangents to the astroid, take the normal to each tangent from the origin, and then plot the locus of the feet of such normals
To construct the pedal curve of the astroid relative to the origin O, we simply construct the tangents to the astroid, take the normal to each tangent from the origin, and then plot the locus of the feet of such normals