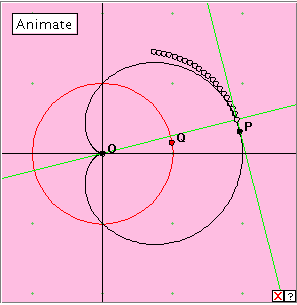
cardioid :pedal curve

CARDIOID : Pedal curve

We construct the pedal curve of the cardioid relative to the cusp point O.

Click the linked diagram below and then the ‘Animate’ button to generate the pedal curve of the cardioid. Click the button again to stop the generation. Describe the mechanics of this generation. Clicking the little x at bottom right will clear the drawing from the applet window. Now try dragging the drive point Q rapidly around the circle. You might like to try defining the generated pedal curve here, but it is a bit tricky!

This cardioid has equations x = a(1 + cos t) cos t, y = a(1 + cos t) sin t.

You could be forgiven for suggesting that the pedal curve of the cardioid generated here is a limaçon. It would not be out of place here, and has the right sort of shape. However, it is a curve having a different equation, and is known as Cayley’s sextic. This curve was actually discovered by Scottish mathematician Colin Maclaurin, but was first studied in detail by Arthur Cayley.

BIBLIOGRAPHY

Wolfram MathWorld : http://mathworld.wolfram.com/CardioidPedalCurve.html

Cayley’s sextic : http://mathworld.wolfram.com/CayleysSextic.html