|
CYCLOID : Pedal Curve
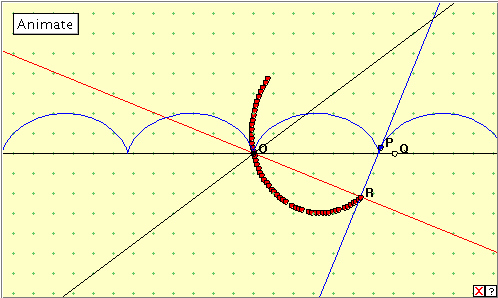
We recall the cycloid as the path traced out by a point on a circle rolling along a straight line. To find the pedal curve of the cycloid relative to the origin O, we draw in the normals from O to the tangents to the curve and plot the points of intersection. Click the linked figure below, and then click the ‘Animate’ button to generate the pedal curve of the cycloid. Click the button again to stop the generation. You can also see the construction by manually dragging the green point Q along the x-axis. Do you understand the construction? Do you recognize the evolute? Can you name it? describe it? |