|
 We have already looked at the deltoid as a type of three-pointed ornamental star. As usual, to find the pedal curve from a point K, we take the normals from K to the tangents to the deltoid, and plot the points of intersection of tangents and corresponding normals. We have already looked at the deltoid as a type of three-pointed ornamental star. As usual, to find the pedal curve from a point K, we take the normals from K to the tangents to the deltoid, and plot the points of intersection of tangents and corresponding normals.
Click on the diagram below to open the applet, and then click on the ‘Animate’ button to generate the pedal curve of the deltoid. Clicking the little red x at bottom right will clear the drawing from the applet window. Now drag the red point Q once slowly around the circle. Can you describe the pedal curve construction? Is this a curve we have seen before? Experiment with different positions of point K on the x-axis. In particular you might look at the cases where K is at the centre, at a cusp, or simply ‘on the curve’. I can generate a pretty convincing fish!
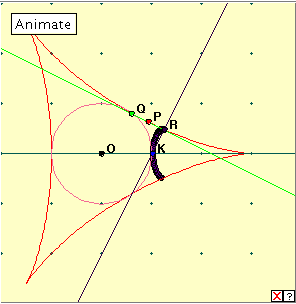
When K is at the centre O, the pedal curve generated is a three-petal ‘flower’ called a trifolium. We would expect this pedal curve to have three fold symmetry. Why? When K lies at a cusp, we get a single ‘petal’ or simple folium, and when K lies at the simple intersection of the deltoid and the x-axis, we get a bifolium. You might like to investigate other possibilities.
Biography
http://mathworld.wolfram.com/DeltoidPedalCurve.html
|
 We have already looked at the deltoid as a type of three-pointed ornamental star. As usual, to find the pedal curve from a point K, we take the normals from K to the tangents to the deltoid, and plot the points of intersection of tangents and corresponding normals.
We have already looked at the deltoid as a type of three-pointed ornamental star. As usual, to find the pedal curve from a point K, we take the normals from K to the tangents to the deltoid, and plot the points of intersection of tangents and corresponding normals.