|
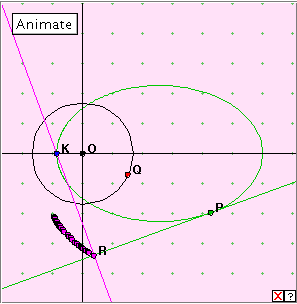
ELLIPSE : Pedal curve
In this case we take the ellipse as a point locus, and construct the normal from point K to the tangent at each point of the curve. The envelope of these constructed intersection points then generates the required pedal curve. For this curve we obtain some familiar-looking curves as pedal curves. When K lies at a focus the pedal curve is a circle. When K lies on or outside the ellipse, the pedal curve looks like a cardioid or limaçon, but it appears that in fact it is not. Bibliography |