We take the locus of the lemniscate, and draw the normal from the centre O to the tangent at each point of the locus. The pedal curve with respect to O is the locus of the points of intersection of tangent and corresponding normal.

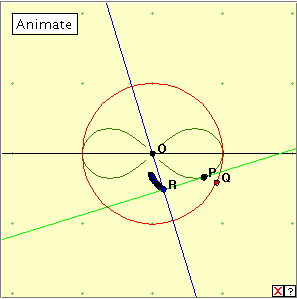
In the applet linked below, as Q traverses the red circle, point P describes the lemniscate. The pedal curve occurs as the locus of the point R. Press the ‘Animate’ button to generate the pedal curve. You can delete this construction by clicking on the red cross at lower right. A fuller representation of the locus can be found by manually dragging the point Q around the red circle. Can you identify the pedal curve here? What does it look like?