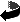The parabola is a member of the family of conics. The pedal curve construction with respect to the variable point K gives rise to a number of recognizable curves. As usual, we take the normals from K to the tangents to the parabola, and plot the locus of the intersection points.

Click the diagram below to activate the applet, and then click the ‘Animate’ button, or manually drag the red driver point along the x-axis. We have extended the range of this point well beyond the edges of the applet window in order to generate the pedal curves. Investigate this situation for various positions of the base point K. Obvious points to look at closely are the origin, the interesections of the directrix with the x-axis, the focus. Can you identify these pedal curves?

When K lies at the focus, the pedal curve is a straight line. (What is this straight line, and why would we expect this result?) If K is the intersection of the directrix with the x-axis, we obtain the right strophoid. When K lies at the vertex of the parabola, the pedal curve is the vurve known as the cissoid of Diocles. There is another pedal curve of interest. This occurs when K lies at the reflection of the focus F in the directrix (two dots to the left of the red line on the x-axis). This curve is the trisectrix of Maclaurin, historically used to trisect an angle.




Bibliography

http://mathworld.wolfram.com/ParabolaPedalCurve.html