In this section we give java applets which generate some of the pedal curves of each of our curves.
The pedal curve of a curve S is easily defined. Let S be the given curve, and let Q be a given fixed point. For any tangent t to the curve S, let the normal from Q to t meet the tangent at point P. Then the locus of point P is the pedal curve of Q with respect to curve S.
Notice that P is the foot of the normal from Q, and the word pedal means foot (compare the pedal of a bicycle).
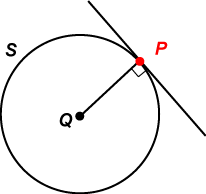 As a trivial example, if curve S is a circle, and point Q is the centre of the circle, then the pedal curve of Q with respect to the circle is the circle itself. This is because for each tangent to the circle, the normal from the centre meets the tangent on the circle. Thus the locus of the red points P is the circle.
As a trivial example, if curve S is a circle, and point Q is the centre of the circle, then the pedal curve of Q with respect to the circle is the circle itself. This is because for each tangent to the circle, the normal from the centre meets the tangent on the circle. Thus the locus of the red points P is the circle.
We shall look for some more interesting pedal curves!
Bibliography
A book of curves, Lockwood, E. H. (Cambridge University Press 1967).