|
TRACTRIX : Exploration
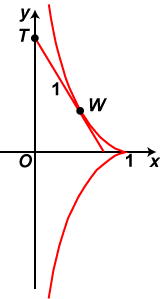
Suppose we have a weight W, placed (say) at the cusp point of the tractrix (see graph below). A string of length 1 is attached to the weight, and initially reaches down to the origin. The free end T is now steadily pulled in a vertical direction along the y-axis. The weight W then traces out a branch of the tractrix. To see why this occurs, first Notice that TW = 1, the length of the string. Also, we expect TW to be tangent to the curve at W, since the wight W will always be pulled directly towards T. Using the notation of the (modified) figure, and in particular the triangle TVW, we see that the slope of the tangent at W is given by
We also have y(0) = 1. Solving this differential equation gives the rather unpleasant Cartesian equation of the tractrix as
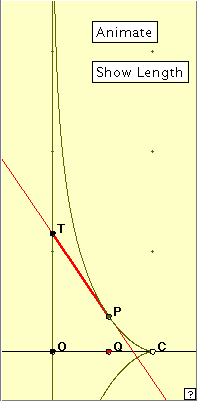
The The parametric equations are not much better : x = log (sec t + tan t) – sin t , y = c cos t , where 0 Fortunately the programmer has only to enter in the formulae – not do any hard manipulation! We notice that in this position the tractrix has a right pointing cusp on the x-axis, and the y-axis is an asymptote to the curve: as y gets infinitely large positive or negative, the tractrix curve approaches the axis more and more closely. You might like to think of it as a double tangent ‘at infinity’.
The diagram at right shows one branch of the tractrix, a point P on the branch, and a tangent to the curve at P meeting the asymptote at point T. Play with the applet. Moving Q manually is probably more helpful than using the ‘Animate’ button. Do you notice anything about the length of segment PT? Can you conjecture a value here? (Notice that OC = 1.) Why would you expect this property to be true? Now click on the ‘Show Length’ button to check your result. In spite of the measured lengths(!) we expect the length here to be 1. It is of course the length of the string in the original setting up of the problem. We would also expect the applet to fail at the cusp point C itself, since no tangent is defined at this point. We have then the result: The length of the intercept of a tangent to the tractrix from the contact point P to the asymptote is constant, and equals OC.
http://demonstrations.wolfram.com/ and do a site search for ‘tractrix’. Here is a delightful (and elaborate) applet which demonstrates this property. BIBLIOGRAPHY |
As we have seen from the ‘Generation’ tractrix page, a branch of the tractrix arises in connection with a physical problem where a weight is pulled along. In fact, the name ‘tractrix’ comes from the Latin verb trahere ’to pull, drag‘.
signs allow for the pulling point T to move up or down the y-axis, generating both branches of the tractrix. This equation has various other equivalent forms, some involving the hyperbolic cosine.
t < 2
.
