|
TRACTRIX : Generation
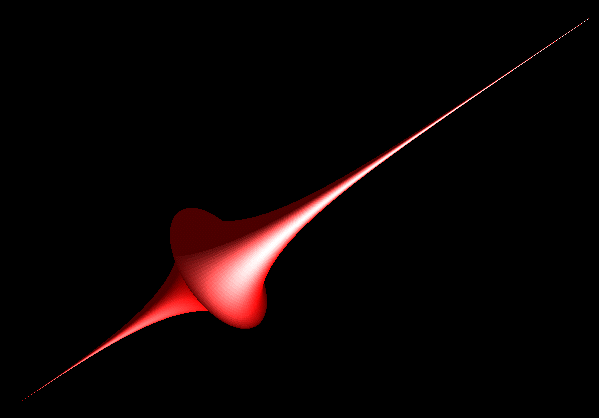
To see this, modify the graph ... . Question: What is the path traced out by the weight W? No prizes for the right answer here! But it was more of a problem when it was first introduced by Claude Perrault in 1670, and then later studied by Sir Isaac Newton (1676) and Christian Huygens(1692). The required path is the top branch of the tractrix. OCCURRENCES The sculpture below left was created by Robert R. Wilson and is called 'Tractricious'. We’ll have to take it on trust that it is not a hyperboloid of one sheet! By far and away the most common occurrence of the tractrix is in the design of audio speakers, and the so-called ‘tractrix horn’. A large version is shown below centre. The tractrix is also of mathematical interest in the construction of the pseudosphere, below right. We see that this is a solid of revolution, obtained by revolving a tractrix about its asymptote. Although it looks nothing like a sphere, there is a link. A sphere is a body which has constant positive curvature; the pseudosphere is a body which has constant negative curvature.
|
As with the catenary, there is no simple method of generating the tractrix. In fact, as a curve, the tractrix appears to be even more reclusive and elusive than the catenary. However, the tractrix does have a natural occurrence which we describe below. It is also related to the catenary: we this later, when we investigate the relationships between the various plane curves.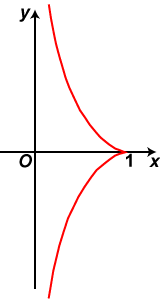
The tractrix arises in connection with a physical problem. Suppose we have a weight W, placed (say) at the cusp point of the tractrix (see graph at right). A string of length 1 is attached to the weight, and initially reaches across to the origin. The free end T is now steadily pulled upwards along the y axis, dragging the weight after it.
