1. SPECIAL TRIANGLE POINTS
We begin by looking at three special points which are associated with any triangle in the plane, and an interesting property they share. These points are the circumcentre, orthocentre, and centroid.
Let
Can you prove this? Referring to the diagram, use two of the perpendicular bisectors to determine O, then drop a perpendicular from O to the third side of the triangle. What needs to be proved? Perhaps you need a further hint? |
| The perpendicular bisector of a chord AB is the locus of points which are equidistant from A and B. It is a straight line which is perpendicular to AB, and passes through the midpoint of AB. |
|
The perpendicular bisectors of the sides at A', B', C' meet in the point O. In order to prove this we take the perpendicular bisectors C'O and B'O of sides AB and AC to meet in O, and drop the perpendicular OA' to side BC. Our result will be proved if we can show that A' is the midpoint of side BC. Proof OB = OA (since OC' perpendicularly bisects AB) Now OB = OC implies that O lies on the perpendicular bisector of BC. Hence OA' is the perpendicular bisector of BC and A' is the midpoint of BC as required. This completes the proof. We observe that since OA = OB = OC, O is the centre of the (unique) circumcircle which passes through the vertices of the triangle. O is thus called the circumcentre of the triangle. |
Orthocentre
Can you prove this? There are various ways of establishing this result, none of them very obvious. However, there is a very clever simple proof, which comes with a hint! We notice that the altitudes are line segments which are perpendicular to the sides of the triangle. In our work on circumcentre, we found a result about lines which had this property. So, could we create a new triangle, somehow related to the given When you think you have the answer, check it out here. |
| An altitude of a triangle is the line segment drawn from any vertex to meet the opposite side of the triangle at right angles. The word is sometimes also used to denote the length of such a segment, particularly when the relevant ‘opposite side’ is described as the base of the triangle. |
The altitudes of triangle ABC meet in a point H called the orthocentre. As in the diagram, construct Now since the opposite sides of a parallelogram have equal length, C"A = BC = AB", so A is the midpoint of B"C". Thus AH is the perpendicular bisector of side B"C" of Hence the altitudes AD, BE, CF of What a clever and easy way of obtaining this result!
|
| The prefix ortho is used mathematically to mean ‘right’ as in ‘orthogonal’ for two lines meeting at a right angle. Curiously, its normal meaning is ‘straight’ as in ‘orthodox’ (= ‘straight’ doctrine) or ‘orthoptics’ (= the study of straightening eyes). |
Let The segments AA', BB', CC' are called the medians of the triangle. We claim that:
See if you can prove this. It is not hard, and there are various possible methods. You might try showing that G divides a median in the ratio 2:1. Click here for a helpful hint ... |
The medians of triangle ABC meet in a point G called the centroid. Hint: the diagram gives a good start to one method of establishing this result. Can you show that BG = 2GB' ? Proof Start with |
| Suppose we have two parallel lines and a common transversal (crossing line).
When lines l and m are parallel, a and b are called corresponding angles, b and c are alternate angles. It is an axiomatic property of parallel lines that a = b, and b = c. In any case, a and c are called vertically opposite angles, and a = c. |
| Theorem: The segment joining the midpoints of two sides of a triangle is parallel to the base and equal to half its length.
Proof Since we know more about parallel lines, we try working backwards.
Hence AQ = RP = QC. So a line through R parallel to the base passes through midpoint Q. Since midpoint Q has a unique position, the first part of the theorem is proved. Also, RQ = BP = PC, so BC = 2 RQ as required.
|
Euler Line
For
From our work thus far, The ratio 2:1 follows from the fact that |
The best way to come to grips with this sort of geometry is just to play with it. Here are some simple exercises. See if you can provide the answers. 1. Show AH = 2A'O. 2. G is the centroid of 3. A is the orthocentre of 4. Is it possible for any two of the three ‘triangle points’ to coincide? What happens to the third point in this case? 5. Show that GH = 2 GO by considering 6. The triangle A"B"C" is constructed as before by drawing parallel lines to the sides of |
 Hints and Solutions Hints and Solutions1. Show AH = 2A'O. 2. G is the centroid of 3. A is the orthocentre of 4. Is it possible for any two of the three ‘triangle points’ to coincide? What happens to the third point in this case? 5. Show that GH = 2 GO by considering 6. The triangle A"B"C" is constructed as before by drawing parallel lines to the sides of |
 Circumcentre
Circumcentre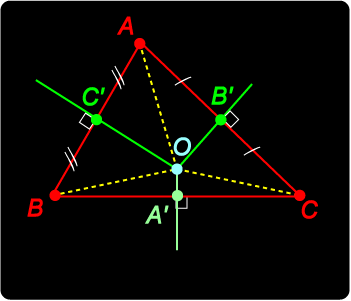 We
We  Let
Let  We
We 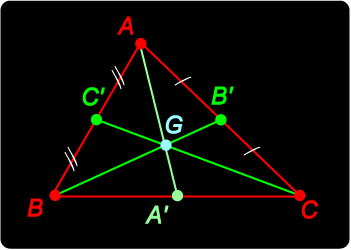 Centroid
Centroid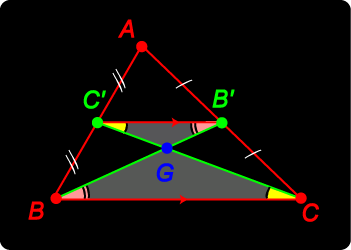 We
We 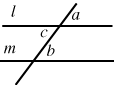
 Let ABC be a given triangle, R the midpoint of AB, and
Let ABC be a given triangle, R the midpoint of AB, and 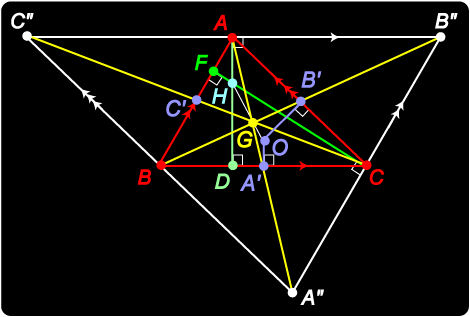 Our diagram is starting to look quite ridiculous!
Our diagram is starting to look quite ridiculous!