10. THE RADICAL AXIS
|
Suppose A, B, C, D are four points in any order on a straight line. We claim:
To establish this we rather cheekily assume the existence of the points X, Y and the midpoint M of XY. We shall give each point the obvious coordinate with respect to some choice of origin O, and find x, y and m in terms of a, b, c and d. We want (a – m)(b – m) = (c – m)(d – m) This gives m = (ab – cd) / (a + b + c + d). So given a, b, c, d, we can calculate m, establishing the existence of a unique point M. If we take M to be the origin, m = 0, and ab = cd. From (*) we now get x2 = y2 = ab = cd, enabling us to calculate x and y. This places the points X, Y distant &Mac195;(ab) = &Mac195;(cd) on either side of M. Thus X and Y exist and this completes the proof. Comments: Since ab may be negative, it is possible that for some arrangements of the points, x and y may be ‘imaginary’. Also, in calculating m there is the possibility that a + b + c + d = 0. You might investigate the placing of the points in this case. |
Now suppose our two non-intersecting circles with centres O, Q meet the common diameter OQ in points A, B; C, D as in the diagram. As in Lemma 10.1, construct points X, Y which are harmonic conjugates to each of the pairs A, B; C, D. We prove
Proof Let P have equal powers with respect to the two circles. We must show that for all such points P, PX = PY. We do this by showing that PX = t where t is the common tangent length from P to the circles. |
P
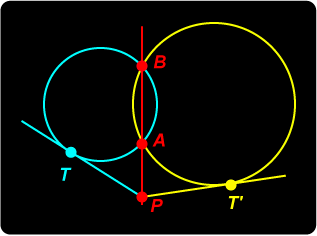 Summing Up Summing UpIn the case of the intersecting circles, we looked at the common chord. We notice that for points lying on the portions of the common chord which lie outside both circles, the tangents to the circles have equal length. The radical axis is thus a sort of extension of the common chord for the case where the circles do not intersect. In fact, the existence of the tangent is really quite irrelevant to the argument: the critical quantity is actually the power of P with respect to the two circles, It is common to use the term radical axis to cover all these cases. The argument we used previously about the common chords of three intersecting circles meeting in a common point carries staraight over here, giving:
The points X, Y used in our argument above are called the limiting points of the two circles. We shall see later that there is good reason for this choice of name. |
Extensions 1. If two circles have two tangents in common, prove that these tangents are bisected by the radical axis. |
P
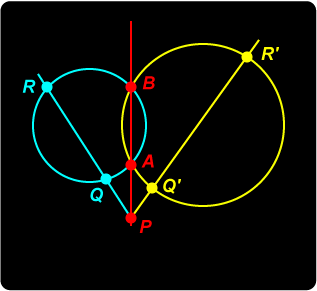 Exploring
Exploring  A Harmonic Problem
A Harmonic Problem Radical Axis
Radical Axis