3. INCIRCLE AND EXCIRCLES
The circumcircle of a triangle is the circle determined by, and passing through, the three vertices of the triangle. Now in the plane, there is a partial duality: an interchange of points and lines.
Given triangle ABC, can you suggest a circle which is determined by the three sides of the triangle? In fact, is there more than one such circle? How many? The centre of the circumcircle is the point of intersection of the three perpendicular bisectors of the sides of the triangle. How would you determine the centres of these new circles? And are these centres related in any nice way? Draw some diagrams of your own and explore these ideas. When you have made as much progress as you can, check your results. |
We can associate with any triangle ABC, an incircle (inscribed circle) which lies within the triangle and has the three sides of the triangle as tangents, and three excircles (escribed circles) which also have the three sides of the triangle as tangents, but which lie exterior to the triangle. We take the centres of these circles to be I, I1, I2, I3 respectively as in the diagram.
Now, how do we locate the centres of these circles? Let's start with the incentre. In this diagram, the two right-angled triangles PIB, RIB have IB in common, and PI = RI. We deduce that these two triangles are congruent,
We can similarly show that each excentre lies at the intersection of one internal bisector and two external bisectors of the angles of the triangle. Finally, is there any nice relationship between the incentre and the three excentres? |
| You might notice we are here using the despised A.S.S. rule which we indicated before as being invalid! In fact this rule is valid for precisely one situation, and that is when the angle being used is a right angle.
In the bottom figure there are again two possibilities, but they are congruent triangles. |
Look now at the adjacent diagram. Points I3, A, I2 are collinear since AI3 and AI2 are bisectors of vertically opposite angles. Similarly for the other sides of this triangle. Points A, I and I1 are collinear, since I and I1 lie on the same bisector of the angle at A. Similarly for the lines through B and C meeting at I. Now look for example at the underlying (pale) angles at A. Now there's a nice surprise! |
1. We have shown that I is the orthocentre of 2. Can you find the nine-point circle of 3. Consider 4. Is it possible for the incentre to be the centroid of a triangle? the orthocentre? the circumcentre? (Use your answer to Q3.)
|
|
1. We have shown that I is the orthocentre of 2. Can you find the nine-point circle of 3. Consider 4. Is it possible for the incentre to be the centroid of a triangle? the orthocentre? the circumcentre? (Use your answer to Q3.) |
 Exploring
Exploring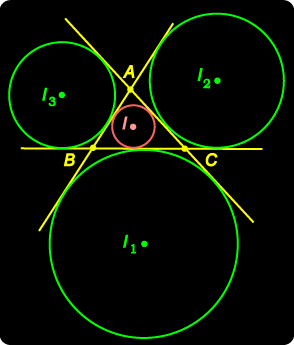 The Incircle and Excircles
The Incircle and Excircles In the top figure at right, we see that the criterion allows for two non-congruent possibilities.
In the top figure at right, we see that the criterion allows for two non-congruent possibilities. 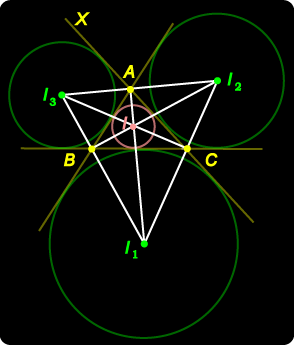 We have asked if there is any
We have asked if there is any