4. THREE INTERSECTING
CIRCLES
The intersection points of two intersecting circles determine a straight line. What happens if we have three intersecting circles?
Exploring We need first to examine an interesting property of the circle. Let P be a point external to a given circle, and let a line through PQR meet the circle in points Q, R. Also, let PT be tangent to the circle at T as in the diagram. Reproduce a copy of this diagram with a larger scale, and for different lines PQR, measure PQ, PR. Tabulate your results as below. What appears to be true?
|
Power of a Point The evidence points to the result: PQ.PR = PT 2. |
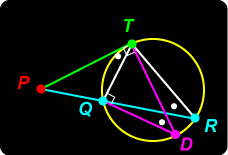 It is easy to see why these two angles must be equal. |
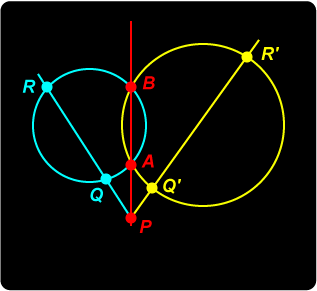 Consider two circles intersecting in points A, B. The line AB is called the radical axis of the two circles. It has a special property. Consider two circles intersecting in points A, B. The line AB is called the radical axis of the two circles. It has a special property.Let P be an arbitrary point on AB. What can you say about PQ . PR? What can you say about PQ' . PR' ? Why are these two quantities equal? We see that PQ . PR = PA . PB (power property of the blue circle) = PQ'. PR' (power property of the yellow circle). So point P has the same power with respect to both circles. Notice that the argument still holds if P lies at an intersection of the circles, or on the line segment AB. Thus
Now what happens if we have three intersecting circles? |
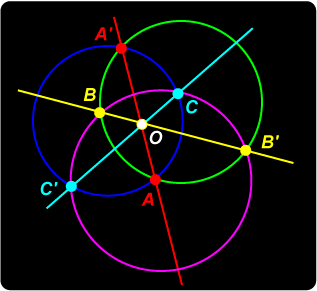
Three Intersecting Circles
Proof To prove this assertion, suppose that axes BB' and CC' meet in O. Does AA' also pass through O? Since O lies on BB', O has the same power with respect to the green circle and the magenta circle. Since O lies on CC', O has the same power with respect to the blue circle and the magenta circle. Hence, O has the same power with respect to the green circle and the blue circle. Hence O lies on the radical axis AA' of these two circles. Thus the three radical axes meet in the common point O. |
1. Let C be a circle of radius r and centre O. Sometimes the power of P with respect to C is defined as OP 2 – r 2. How does this compare with the definition we have given? What happens when P lies inside the circle? on the circle? |
 Hints and Solutions Hints and Solutions1. Let C be a circle of radius r and centre O. Sometimes the power of P with respect to C is defined as OP 2 – r 2. How does this compare with the definition we have given? What happens when P lies inside the circle? on the circle? |