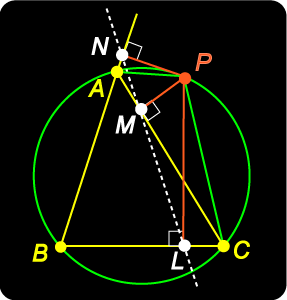
5. THE SIMSON LINE


Robert Simson (1687 – 1768) was a Scottish mathematician who made many discoveries in geometry, and the Simson line is named after him. However, the Simson line does not appear in any of his published work, and appears to have been discovered by William Wallace! That’s life ... .

Exploring

You are given any triangle ABC and P an arbitrary point of its circumcircle.
Points L, M, N on the sides BC, CA, AB (possibly extended) are chosen so that PL BC, PM CA and PN AB as in the diagram.

     Can you make any conjecture about the points L, M, N ?
     Draw some other diagrams with different positions of the point P.

Check ...


Do some further exploration with this Java applet ...

In what follows we shall need a property of cyclic quadrangles:

the opposite angles of a cyclic quadrangle add to 180°.

                                 

The opposite angles of a cyclic quadrangle add to 180°.

This property follows easily from our previous result that the angle subtended by a chord PQ at the circumference is twice the angle subtended at the centre O of the circle. Since the green and blue angles at the centre add to 360°, the sum of the green and blue angles at the circumference add to 180°.

It is also true that if the opposite angles of a quadrangle add to 180°, then the quadrangle is cyclic.





























The Simson Line

We have the following theorem:

Point P lies on the circumcircle of ABC the feet L, M, N of the perpendiculars from P to the sides BC, CA, AB of the triangle lie on a straight line (the Simson line of the triangle).

Proof: () Let us suppose that P lies on the circumcircle of ABC.
We must show that points L, M, N are collinear.
To do this, we allow the possiblity that line LMN is ‘bent’ at M,
and show that PMN + PML = 180°.

Now PMN = PAN (cyclic quadrangle PMAN,
                                            angles subtended by chord PN)
                     = 180° – PAB (adjacent angles on side BAN)
                     = PCB (cyclic quadrangle PABC,
                                            opposite angles add to 180°)
                     = PCL (just renaming the angle)
                     = 180° – PML (cyclic quadrangle PCLM, opposite angles add to 180°).

This establishes our result. Thus, L, M, N lie on a straight line.

We now establish the result in the opposite direction ().

                                 
































The Converse

We have the following theorem:

Point P lies on the circumcircle of ABC the feet L, M, N of the perpendiculars from P to the sides BC, CA, AB of the triangle lie on a straight line (the Simson line of the triangle).

Proof: () Let us suppose that points L, M, N are collinear.
To show that point P lies on the circumcircle of the triangle, we show that PAB + PCB = 180° (that is, that points P, A, B, C are concyclic). The proof rearranges the steps of our original proof.

Now PCB = PCL (just renaming)
                     = 180° – PML (cyclic quadrangle PMLC,
                                                     opposite angles add to 180°)
                     = PMN (adjacent angles on straight straight line LMN
                                                     add to 180°)
                     =  PAN (cyclic quadrangle PMAN, angles subtended by PN)
                     = 180° – PAB (adjacent angles on straight line BAN add to 180°).

This establishes our result. Thus, P lies on the circumcircle of ABC .

                                   




































P

Extensions

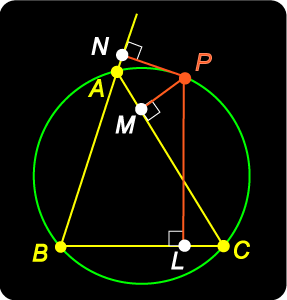
1. Let PM meet the circumcircle again in the point M'. What may be true about the line BM' and the Simson line? Can you prove this? What other lines have this property?

2. Let H be the orthocentre of ABC. Let the altitude through A and H meet the circumcircle again in D', and let PD' meet BC in X. Can you conjecture a relationship between HX and the Simson line? Can you prove it? Use this figure.

3. Consider the relationship of PH to the Simson line. What appears to be true? Can you prove it?

There are many more interesting results in this fascinating diagram!

                                                                 Hints and Solutions ...

For looking up ...

http://en.wikipedia.org/wiki/Simson_line

http://mathworld.wolfram.com/SimsonLine.html

Geometry for Advanced Pupils, Maxwell, E. A. (Oxford 1963)  
                                                                                                                                                                                 












































P
Hints and Solutions

1. Let PM meet the circumcircle again in the point M'. What may be true about the line BM' and the Simson line? Can you prove this?
What other lines have this property?

• BM' // LMN. PM'B is supplementary to PCB which is
   supplemnetary to PML (cyclic quadrangle PMLC).
   Hence PML = PM'B and BM' // LMN. Similarly for CN', AL'.

2. Let H be the orthocentre of ABC. Let the altitude AD through H meet the circumcircle again in D', and let PD' meet BC in X. Can you conjecture a relationship between HX and the Simson line?
Can you prove it? Use this figure.

• First use congruent triangles to show HD = DD'.
   Now let PL meet the circle again in L'.
   Verify that L'AD' = PD'A = XHD'. So HX // AL'.

3. Consider the relationship of PH to the Simson line. What appears to be true? Can you prove it?

•  It appears that the Simson line LMN bisects PH. Extend HX to meet PL' in point P'.
   Then triangles PLX and P'LX are congruent (noting that HDX D'DX above). So PL = P'L.
   We also know LMN // HXP', so line LMN cuts off equal intercepts on transversal PH. That is, LMN bisects PH.